
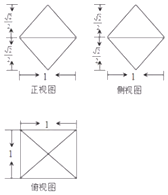
| A. | $\frac{{\sqrt{2}}}{3}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $4\sqrt{3}$ |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,0) | B. | {-3,-2,-1} | C. | {-3,-2,-1,0,1} | D. | {-3,-2,-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
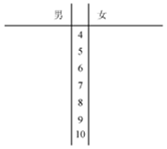 某学校对男女学生进行有关“习惯与礼仪”的调查,分别随机抽查了18名学生进行评分(百分制:得分越高,习惯与礼仪越好),评分记录如下:
某学校对男女学生进行有关“习惯与礼仪”的调查,分别随机抽查了18名学生进行评分(百分制:得分越高,习惯与礼仪越好),评分记录如下:| 等级 性别 | 较差 | 较好 | 合计 |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 | K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$ |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 三维柱形图 | B. | 二维条形图 | C. | 等高条形图 | D. | 独立性检验 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
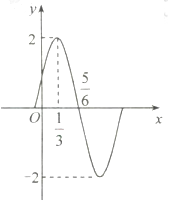 已知函数$f(x)=Asin({ωx+ϕ})({A>0,ω>0,|ϕ|<\frac{π}{2}})$的图象(部分)如图所示.
已知函数$f(x)=Asin({ωx+ϕ})({A>0,ω>0,|ϕ|<\frac{π}{2}})$的图象(部分)如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com