
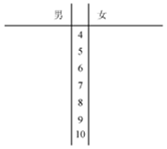
 ijѧУ����Ůѧ�������йء�ϰ�������ǡ��ĵ��飬�ֱ���������18��ѧ���������֣��ٷ��ƣ��÷�Խ�ߣ�ϰ��������Խ�ã������ּ�¼���£�
ijѧУ����Ůѧ�������йء�ϰ�������ǡ��ĵ��飬�ֱ���������18��ѧ���������֣��ٷ��ƣ��÷�Խ�ߣ�ϰ��������Խ�ã������ּ�¼���£�| �ȼ� �Ա� | �ϲ� | �Ϻ� | �ϼ� |
| ���� | |||
| �� | |||
| �ϼ� |
| P��K2��k�� | 0.050 | 0.010 | 0.001 | ��K2=$\frac{n��ad-bc��^{2}}{��a+b����c+d����a+c����b+d��}$ |
| k | 3.841 | 6.635 | 10.828 |
���� ��1����д��Ҷͼ��ͨ����Ҷͼ�е�����֪��
������ϰ�������ǡ����ֵ�ƽ��ֵС��Ů����ϰ�������ǡ����ֵ�ƽ��ֵ��
��������ϰ�������ǡ����ַ�ɢ�̶Ƚϴ�Щ��
��2����д2��2������������۲�ֵK2���Ƚϵó����ۣ�
��� �⣺��1����ʮλ����Ϊ������λ����ΪҶ��������Ҷͼ����ͼ��ʾ��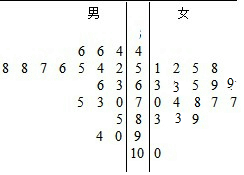
ͨ����Ҷͼ֪��������ϰ�������ǡ����ֲַ���44��94֮�䣬�Ҽ�����46��66֮�䣻
Ů����ϰ�������ǡ����ֲַ���51��100֮�䣬�Ҽ�����51��83֮�䣻
���ԣ�������ϰ�������ǡ����ֵ�ƽ��ֵС��Ů����ϰ�������ǡ����ֵ�ƽ��ֵ��
��������ϰ�������ǡ����ַ�ɢ�̶Ƚϴ�Щ��
��2����д2��2��������
| �ȼ� �Ա� | �ϲ� | �Ϻ� | �ϼ� |
| ���� | 10 | 8 | 18 |
| �� | 4 | 14 | 18 |
| �ϼ� | 14 | 22 | 36 |
���� ���⿼���˾�Ҷͼ������Լ����Ӧ�����⣬Ҳ�����˷�������������������ǻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
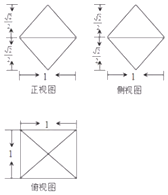
| A�� | $\frac{{\sqrt{2}}}{3}$ | B�� | $\sqrt{3}$ | C�� | $2\sqrt{3}$ | D�� | $4\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
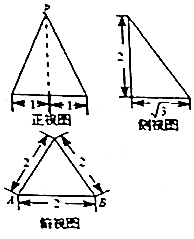
| A�� | $\sqrt{7}$ | B�� | 2 | C�� | 1 | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
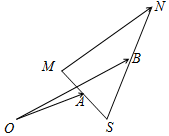 ��ͼ����֪$\overrightarrow{OA}$=$\overrightarrow{a}$��$\overrightarrow{OB}$=$\overrightarrow{b}$�������M���ڵ�A�ĶԳƵ�ΪS����S���ڵ�B�ĶԳƵ�ΪN��������$\overrightarrow{MN}$=2$\overrightarrow{b}$-2$\overrightarrow{a}$����$\overrightarrow{a}$��$\overrightarrow{b}$��ʾ����$\overrightarrow{MN}$��
��ͼ����֪$\overrightarrow{OA}$=$\overrightarrow{a}$��$\overrightarrow{OB}$=$\overrightarrow{b}$�������M���ڵ�A�ĶԳƵ�ΪS����S���ڵ�B�ĶԳƵ�ΪN��������$\overrightarrow{MN}$=2$\overrightarrow{b}$-2$\overrightarrow{a}$����$\overrightarrow{a}$��$\overrightarrow{b}$��ʾ����$\overrightarrow{MN}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com