
分析 由$\left\{\begin{array}{l}{x=-3+t}\\{y=1+\sqrt{3}t}\end{array}\right.$,消去参数t,得普通方程,求出直线的斜率,即可求倾斜角.
解答 解:由$\left\{\begin{array}{l}{x=-3+t}\\{y=1+\sqrt{3}t}\end{array}\right.$,消去参数t,
得普通方程$\sqrt{3}$x-y+3$\sqrt{3}$+1=0,
k=$\sqrt{3}$=tanα,
∴α=$\frac{π}{3}$,
因此直线l的倾斜角为$\frac{π}{3}$.
点评 本题考查了参数方程化为普通方程的方法,考查了推理能力与计算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 5 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,0) | B. | {-3,-2,-1} | C. | {-3,-2,-1,0,1} | D. | {-3,-2,-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
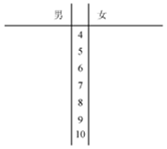 某学校对男女学生进行有关“习惯与礼仪”的调查,分别随机抽查了18名学生进行评分(百分制:得分越高,习惯与礼仪越好),评分记录如下:
某学校对男女学生进行有关“习惯与礼仪”的调查,分别随机抽查了18名学生进行评分(百分制:得分越高,习惯与礼仪越好),评分记录如下:| 等级 性别 | 较差 | 较好 | 合计 |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 | K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$ |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com