
分析 (1)数列{an}的首项为a1=$\frac{1}{4}$,公比q=$\frac{1}{4}$的等比数列,an=$(\frac{1}{4})^{n}$.可得bn=3n-2即可证明.
(2)由(1)知:cn=(3n-2)$•(\frac{1}{4})^{n}$,利用“错位相减法”与等比数列的求和公式即可得出.
解答 (1)证明:数列{an}的首项为a1=$\frac{1}{4}$,公比q=$\frac{1}{4}$的等比数列,an=$(\frac{1}{4})^{n}$.
∵bn+2=3log${\;}_{\frac{1}{4}}$an(n∈N*),∴bn=3n-2是关于n的一次函数,
因此:{bn}是等差数列,首项为1,公差为3.
(2)由(1)知:cn=(3n-2)$•(\frac{1}{4})^{n}$,
∴Sn=$1×\frac{1}{4}+3×(\frac{1}{4})^{2}$+$7×(\frac{1}{4})^{3}$+…+(3n-2)$•(\frac{1}{4})^{n}$,
$\frac{1}{4}{S}_{n}$=$(\frac{1}{4})^{2}+3×(\frac{1}{4})^{3}$+…+(3n-5)$•(\frac{1}{4})^{n}$+(3n-2)$•(\frac{1}{4})^{n+1}$,
两式相减得$\frac{3}{4}$Sn=$\frac{1}{4}+3[(\frac{1}{4})^{2}+(\frac{1}{4})^{3}$+…+$(\frac{1}{4})^{n}]$-(3n-2)$•(\frac{1}{4})^{n+1}$=$\frac{1}{4}$+3×$\frac{\frac{1}{16}(1-\frac{1}{{4}^{n-1}})}{1-\frac{1}{4}}$-(3n-2)$•(\frac{1}{4})^{n+1}$=$\frac{1}{2}$-(3n+2)×$\frac{1}{{4}^{n+1}}$.
∴Sn=$\frac{2}{3}$-$\frac{12n+8}{3}$×$\frac{1}{{4}^{n+1}}$(n∈N*).
点评 本题考查了“错位相减法”、等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
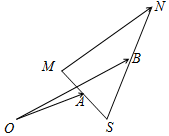 如图,已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,任意点M关于点A的对称点为S,点S关于点B的对称点为N,则向量$\overrightarrow{MN}$=2$\overrightarrow{b}$-2$\overrightarrow{a}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示向量$\overrightarrow{MN}$)
如图,已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,任意点M关于点A的对称点为S,点S关于点B的对称点为N,则向量$\overrightarrow{MN}$=2$\overrightarrow{b}$-2$\overrightarrow{a}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示向量$\overrightarrow{MN}$)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x2 | B. | y=x|x| | C. | y=x+$\frac{2}{x}$ | D. | y=x-$\frac{4}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{7}{8}$ | C. | $\frac{9}{8}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com