
分析 ①求出双曲线的离心率即可判断命题正误;
③通过点到直线的距离得出a,b,c的关系,求出双曲线的离心率判断正误;
③通过∠F1B1A2=90°,转化为a,b,c的关系,求出双曲线的离心率判断正误;
④利用双曲线的简单性质求出离心率,利用黄金双曲线的定义判断正误.
解答 解:对于①,双曲线x2-$\frac{{2{y^2}}}{{\sqrt{5}-1}}$=1中,c2=1+$\frac{\sqrt{5}-1}{2}$=$\frac{\sqrt{5}+1}{2}$,
∴c=$\sqrt{\frac{\sqrt{5}+1}{2}}$,∴离心率e=$\sqrt{\frac{\sqrt{5}+1}{2}}$≠$\frac{\sqrt{5}+1}{2}$,
∴该曲线不是黄金双曲线,①错误;
对于②,双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上一点P(x0,y0)到两条渐近线y=±$\frac{b}{a}$x的距离积;
∴$\frac{|{bx}_{0}+{ay}_{0}|}{\sqrt{{a}^{2}{+b}^{2}}}$•$\frac{|{bx}_{0}-{ay}_{0}|}{\sqrt{{a}^{2}{+b}^{2}}}$=$\frac{{{{|b}^{2}x}_{0}}^{2}{{{-a}^{2}y}_{0}}^{2}|}{{a}^{2}{+b}^{2}}$=$\frac{a^3}{c}$,
∴$\frac{{{a}^{2}b}^{2}}{{c}^{2}}$=$\frac{{a}^{3}}{c}$,即b2=ac,
∴c2-a2-ac=0,化为e2-e-1=0,
又e>1,解得e=$\frac{\sqrt{5}+1}{2}$,∴该双曲线是黄金双曲线,②正确;
对于③,∵∠F1B1A2=90°,∴${{{|B}_{1}F}_{1}|}^{2}$+${{{|B}_{1}A}_{2}|}^{2}$=${{{|F}_{1}A}_{2}|}^{2}$,
∴b2+c2+b2+a2=(a+c)2,化为c2-ac-a2=0,
由②知该双曲线是黄金双曲线,③正确;
对于④,如图所示, MN经过右焦点F2且MN⊥F1F2,∠MON=90°,
MN经过右焦点F2且MN⊥F1F2,∠MON=90°,
∴NF2=OF2,∴$\frac{{b}^{2}}{a}$=c,∴b2=ac,
由②知该双曲线是黄金双曲线,④正确;
综上,正确命题序号是②③④.
故答案为:②③④.
点评 本题考查双曲线性质的灵活运用问题,也考查了a,b,c的关系以及离心率的应用问题,是综合性题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
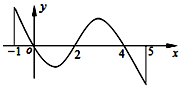 已知函数f(x)定义域为[-1,5],部分对应值如表,f(x)的导函数f′(x)的图象如图所示.
已知函数f(x)定义域为[-1,5],部分对应值如表,f(x)的导函数f′(x)的图象如图所示.| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{3}}{3}$) | B. | ($\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$) | C. | (-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$) | D. | (-$\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{3}}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com