
| A. | y=x2 | B. | y=x|x| | C. | y=x+$\frac{2}{x}$ | D. | y=x-$\frac{4}{x}$ |
分析 根据奇函数、偶函数的定义,分段函数和二次函数的单调性,以及单调区间的连续性即可判断每个选项正误,从而找出正确选项.
解答 解:A.y=x2是偶函数,∴该选项错误;
B.(-x)|-x|=-x|x|;
∴y=x|x|是奇函数;
$y=x|x|=\left\{\begin{array}{l}{{x}^{2}}&{x≥0}\\{-{x}^{2}}&{x<0}\end{array}\right.$;
∴y=x|x|在定义域上是增函数;
∴该选项正确;
C.y=x$+\frac{2}{x}$在定义域上没有单调性,∴该选项错误;
D.$y=x-\frac{4}{x}$的定义域为(-∞,0)∪(0,+∞);
∴该函数在定义域上没有单调性.
故选B.
点评 考查奇函数、偶函数的定义,分段函数及二次函数的单调性,以及函数单调区间的连续性.


科目:高中数学 来源: 题型:选择题
| A. | [-3,0) | B. | {-3,-2,-1} | C. | {-3,-2,-1,0,1} | D. | {-3,-2,-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{3}}{3}$) | B. | ($\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$) | C. | (-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$) | D. | (-$\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{3}}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
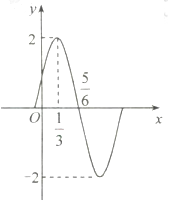 已知函数$f(x)=Asin({ωx+ϕ})({A>0,ω>0,|ϕ|<\frac{π}{2}})$的图象(部分)如图所示.
已知函数$f(x)=Asin({ωx+ϕ})({A>0,ω>0,|ϕ|<\frac{π}{2}})$的图象(部分)如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | 1 | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com