
���� ��1������C�ļ����귽��ת��Ϊ��2=4��cos�ȣ���$\left\{{\begin{array}{l}{{��^2}={x^2}+{y^2}}\\{��cos��=x}\end{array}}\right.$���������C��ֱ�����귽�̣�ֱ��l��ȥ����t�������ֱ��l��ֱ�����귽�̣�
��2����ֱ��l�IJ������̴���x2+y2=4x���ã�${t^2}+\sqrt{3}t-3=0$�����ɵ�Q��3��0����ԲC���ڲ��������||P1Q|-|P2Q||��ֵ��
��� �⣺��1��������C�ļ����귽��Ϊ����=4cos�ȣ����2=4��cos�ȣ�
��$\left\{{\begin{array}{l}{{��^2}={x^2}+{y^2}}\\{��cos��=x}\end{array}}\right.$��x2+y2=4x��
��C��ֱ�����귽��Ϊ����x-2��2+y2=4��
��ֱ��l�IJ�������Ϊ��$\left\{{\begin{array}{l}{x=3+\frac{{\sqrt{3}}}{2}t}\\{y=\frac{1}{2}t}\end{array}}\right.$��tΪ��������
��ֱ��l��ȥ����t��ֱ��l����ͨ����Ϊ��$x-\sqrt{3}y-3=0$��
��2����ֱ��l�IJ������̴���x2+y2=4x���ã�${t^2}+\sqrt{3}t-3=0$��
��P1��P2�Ķ�Ӧ�����ֱ�Ϊt1��t2����${t_1}+{t_2}=-\sqrt{3}��{t_1}{t_2}=-3$��
����3-2��2+02��4������Q��3��0����ԲC���ڲ���
��$|{|{{P_1}Q}|-|{{P_2}Q}|}|=|{|{t_1}|-|{t_2}|}|=|{{t_1}+{t_2}}|=\sqrt{3}$��
���� ���⿼�����ߵ�ֱ�����귽�̡�ֱ�ߵ���ͨ���̵����������߶ε�֮��ľ���ֵ�������е��⣬����ʱҪ�������⣬ע�⼫���ꡢֱ�����껥����ʽ�ĺ������ã�


 A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д� ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7 | B�� | 8 | C�� | 9 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 1 | C�� | -i | D�� | i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | a��c��b | C�� | c��a��b | D�� | c��b��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
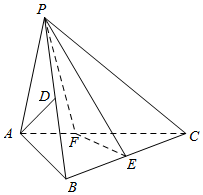 ��ͼ��������P-ABC�У���֪PA=AB����ABCΪֱ�ǣ�PA��BC����D��E�ֱ�ΪPB��BC���е㣮
��ͼ��������P-ABC�У���֪PA=AB����ABCΪֱ�ǣ�PA��BC����D��E�ֱ�ΪPB��BC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com