
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 取AB中点D0,得△ACD0的面积等于△ABC的面积的一半,当经过C点的射线CD位于∠ACD0内部时,满足S△ABC>2S△ACD,因此用∠ACD0的度数除以∠ABC的度数,即得本题的概率.
解答 解:取AB中点D0,得△ACD0的面积等于△ABC的面积的一半.
∵Rt△ABC中,∠C=90°,∠A=30°,
∴CD0=BD0=BC=$\frac{1}{2}$AB,可得∠ACD0=30°
当经过C点的射线CD位于∠SCD0内部时,S△ABC>2S△ACD,
∴所求概率为P=$\frac{30}{90}$=$\frac{1}{3}$.
故选:A.
点评 本题给出含有60°的直角三角形,求射线截三角形所得面积小于直角三角形面积一半的概率,着重考查了几何概型及其计算方法的知识,属于基础题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | {k|k≤-1或k≥1} | B. | {k|-1<k<1} | C. | {k|k<-1} | D. | {k|k≤-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
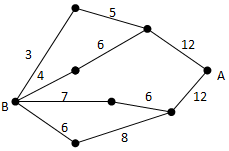 如图,小黑圆表示网络的结点,结点之间的连线表示它们有网线相连.连线上标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )
如图,小黑圆表示网络的结点,结点之间的连线表示它们有网线相连.连线上标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )| A. | 26 | B. | 24 | C. | 20 | D. | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 720 | B. | 120 | C. | 144 | D. | 192 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2,3} | B. | {1,2,3} | C. | {-3,-2,-1,0} | D. | {-3,-2,-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
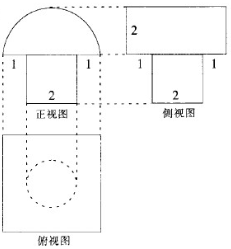
| A. | 20+17π | B. | 20+16π | C. | 16+17π | D. | 16+l6π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com