
【题目】如图,菱形ABCD中,![]() ,
,![]() ,O为线段CD的中点,将
,O为线段CD的中点,将![]() 沿BO折到
沿BO折到![]() 的位置,使得
的位置,使得![]() ,E为
,E为![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)求直线AE与平面![]() 所成角的正弦值
所成角的正弦值
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)根据ABCD为菱形, ![]() ,得到
,得到![]() 为等边三角形,由O为线段CD的中点,得到
为等边三角形,由O为线段CD的中点,得到![]() ,再由
,再由![]() ,得到
,得到![]() ,从而
,从而![]() 平面BOD,得到
平面BOD,得到![]() ,又
,又![]() ,从而
,从而![]() 平面
平面![]() 即可得证.
即可得证.
(2)由(1)知![]() 两两垂直,建立空间直角坐标系,求得平面
两两垂直,建立空间直角坐标系,求得平面![]() 的一个法向量和
的一个法向量和![]() 的坐标,代入公式
的坐标,代入公式 求解.
求解.
(1)因为ABCD为菱形, ![]() ,
,
所以![]() 为等边三角形,
为等边三角形,
又O为线段CD的中点,
所以![]() ,即折叠后有
,即折叠后有![]() ,
,
因为![]() ,所以
,所以![]() ,而
,而![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() 平面BOD,又
平面BOD,又![]() 平面BOD,
平面BOD,
所以![]() ,又
,又![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() .
.
(2)由(1)知![]() 两两垂直,建立如图所示空间直角坐标系:
两两垂直,建立如图所示空间直角坐标系:

则![]()
![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则 ,所以
,所以 ,
,
令![]() ,得
,得![]() ,
,
又因为![]() ,
,
所以 ,
,
所以直线AE与平面![]() 所成角的正弦值
所成角的正弦值![]() .
.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() ,过其右焦点F的直线
,过其右焦点F的直线![]() 交椭圆C于M,N两点,交y轴于E点.若
交椭圆C于M,N两点,交y轴于E点.若![]() ,
,![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)试判断![]() 是否是定值.若是定值,求出该定值;若不是定值,请说明理由.
是否是定值.若是定值,求出该定值;若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在高二年级开设选修课,选课结束后,有6名同学要求改选历史,现历史选修课开有三个班,若每个班至多可再接收3名同学,那么不同的接收方案共有( )
A.150种B.360种C.510种D.512种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为![]() (t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]()
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C相交于A,B两点.求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生活超市有一专柜预代理销售甲乙两家公司的一种可相互替代的日常生活用品.经过一段时间分别单独试销甲乙两家公司的商品,从销售数据中随机各抽取50天,统计每日的销售数量,得到如下的频数分布条形图.甲乙两家公司给该超市的日利润方案为:甲公司给超市每天基本费用为90元,另外每销售一件提成1元;乙公司给超市每天的基本费用为130元,每日销售数量不超过83件没有提成,超过83件的部分每件提成10元.
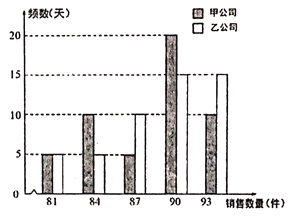
(Ⅰ)求乙公司给超市的日利润![]() (单位:元)与日销售数量
(单位:元)与日销售数量![]() 的函数关系;
的函数关系;
(Ⅱ)若将频率视为概率,回答下列问题:
(1)求甲公司产品销售数量不超过87件的概率;
(2)如果仅从日均利润的角度考虑,请你利用所学过的统计学知识为超市作出抉择,选择哪家公司的产品进行销售?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
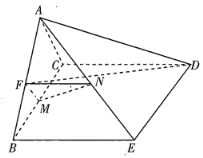
【题目】如图,在四棱锥![]() 中,已知平面
中,已知平面![]() 平面
平面![]() 是边长为2的等边三角形,点
是边长为2的等边三角形,点![]() 是
是![]() 的中点,底面
的中点,底面![]() 是矩形,
是矩形,![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() .
.
(1)若![]() ,点
,点![]() 是
是![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(2)是否存在![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
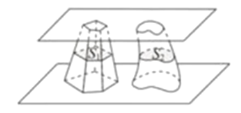
【题目】南北朝时代的伟大数学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”.其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等,如图,夹在两个平行平面之间的两个几何体的体积分别为![]() ,被平行于这两个平面的任意平面截得的两个截面的面积分别为
,被平行于这两个平面的任意平面截得的两个截面的面积分别为![]() ,则“
,则“![]() 总相等”是“
总相等”是“![]() 相等”的( )
相等”的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,SA⊥底面ABC,AC=AB=SA=2,AC⊥AB,D、E分别是AC、BC的中点,F在SE上,且SF=2FE.
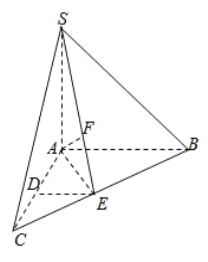
(1)求证:平面SBC⊥平面SAE
(2)若G为DE中点,求二面角G﹣AF﹣E的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com