
【题目】已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,将
的中点,将![]() 沿
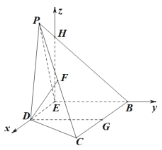
沿![]() 翻折,得到如图所示的四棱锥
翻折,得到如图所示的四棱锥![]() ,且
,且![]() ,设
,设![]() 为
为![]() 的中点.
的中点.
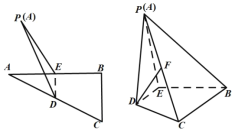
(1)证明:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的的正弦值.
所成角的的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,得到四边形
,得到四边形![]() 是平行四边形,得出
是平行四边形,得出![]() ,
,![]() ,从而
,从而![]() ,
,![]() ,证得
,证得![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,进而利用线面垂直的判定定理,证得
,进而利用线面垂直的判定定理,证得![]() 平面
平面![]() ,即可得到
,即可得到![]() .
.
(2)以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,求得向量
,求得向量![]() 和平面
和平面![]() 的一个法向量,利用向量的夹角公式,即可求解.
的一个法向量,利用向量的夹角公式,即可求解.
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,可得
,可得![]() ,且
,且![]() ,
,
所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,
因为![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,所以
的中点,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,
,
又因为![]() ,且
,且![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() 分别为
分别为![]() 的中点,故
的中点,故![]() ,
,
所以![]() ,又
,又![]() ,
,![]() ,所以
,所以![]() .
.
又因为![]() ,又
,又![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又由![]() 平面
平面![]() ,所以
,所以![]() .
.
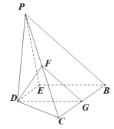
(2)由(1)知:![]() 平面
平面![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,
,
因为![]() ,可得
,可得![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
可得![]() ,所以
,所以![]() ,
,![]() ,
,
所以点![]() 到
到![]() 轴的距离为1,
轴的距离为1,
可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
所以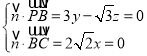 ,解得
,解得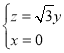 ,令
,令![]() ,可得
,可得![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
则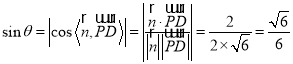 ,
,
即直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】天然气已经进入了千家万户,某市政府为了对天然气的使用进行科学管理,节约气资源,计划确定一个家庭年用量的标准.为此,对全市家庭日常用气的情况进行抽样调查,获得了部分家庭某年的用气量(单位:立方米).将统计结果绘制成下面的频率分布直方图(如图所示).由于操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.若以各组区间中点值代表该组的取值,则估计全市家庭年均用气量约为( )
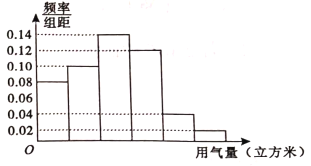
A.6.5立方米B.5立方米C.4.5立方米D.2.5立方米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
②若函数![]() 在
在![]() 上有两个零点,则
上有两个零点,则![]() 的取值范围是
的取值范围是![]() ;
;
③当![]() 时,函数
时,函数![]() 的最大值为0;
的最大值为0;
④函数![]() 在
在![]() 上单调递减;
上单调递减;
上述命题正确的是_________(填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某快递公司收取快递费的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,在收费
的包裹,在收费![]() 元的基础上,每超过
元的基础上,每超过![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.该快递公司承揽了一个工艺品厂家的全部玻璃工艺品包裹的邮寄事宜,该厂家随机统计了
元.该快递公司承揽了一个工艺品厂家的全部玻璃工艺品包裹的邮寄事宜,该厂家随机统计了![]() 件这种包裹的两个统计数表如下:
件这种包裹的两个统计数表如下:
表![]()
包裹重量 |
|
|
|
|
|
包裹数 |
|
|
|
|
|
损坏件数 |
|
|
|
|
|
表![]()
包裹重量 |
|
|
|
|
|
出厂价(元 |
|
|
|
|
|
卖价(元 |
|
|
|
|
|
![]() 估计该快递公司对每件包裹收取快递费的平均值;
估计该快递公司对每件包裹收取快递费的平均值;
![]() 将包裹重量落入各组的频率视为概率,该工艺品厂家承担全部运费,每个包裹只有一件产品,如果客户收到有损坏品的包裹,该快递公司每件按其出厂价的
将包裹重量落入各组的频率视为概率,该工艺品厂家承担全部运费,每个包裹只有一件产品,如果客户收到有损坏品的包裹,该快递公司每件按其出厂价的![]() 赔偿给厂家.现该厂准备给客户邮寄重量在区间
赔偿给厂家.现该厂准备给客户邮寄重量在区间![]() 和
和![]() 内的工艺品各
内的工艺品各![]() 件,求该厂家这两件工艺品获得利润的分布列和期望.
件,求该厂家这两件工艺品获得利润的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某外国语学校举行的![]() (高中生数学建模大赛)中,参与大赛的女生与男生人数之比为
(高中生数学建模大赛)中,参与大赛的女生与男生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖.按女生、男生用分层抽样的方法抽取
)的同学获奖.按女生、男生用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图如图所示.
人的成绩作为样本,得到成绩的频率分布直方图如图所示.
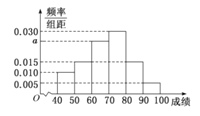
(Ⅰ)求![]() 的值,并计算所抽取样本的平均值
的值,并计算所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)填写下面的![]() 列联表,并判断在犯错误的概率不超过
列联表,并判断在犯错误的概率不超过![]() 的前提下能否认为“获奖与女生、男生有关”.
的前提下能否认为“获奖与女生、男生有关”.
女生 | 男生 | 总计 | |
获奖 |
| ||
不获奖 | |||
总计 |
| ||
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中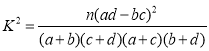 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 上两点,圆
上两点,圆![]() .
.
(1)若![]() 轴,且满足直线
轴,且满足直线![]() 与圆
与圆![]() 相切,求圆
相切,求圆![]() 的方程;
的方程;
(2)若圆![]() 的半径为2,点
的半径为2,点![]() ,
,![]() 满足
满足![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得弦长的最大值.
截得弦长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com