
【题目】如图,四棱锥![]() 中,侧棱
中,侧棱![]() 垂直于底面
垂直于底面![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 平行于
平行于![]() ,
,![]() 平行于面
平行于面![]() ,
,![]() .
.

(1)求![]() 的长;
的长;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,由三角形中位线定理,以及线面平行的判定定理可得
,由三角形中位线定理,以及线面平行的判定定理可得![]() 平行于
平行于![]() ,
,![]() 平行于
平行于![]() ,于是可得
,于是可得![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,![]() ;(2)取
;(2)取![]() 中点
中点![]() ,则
,则![]() 垂直于
垂直于![]() ,以
,以![]() 点为原点,
点为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立坐标系,平面
轴建立坐标系,平面![]() 法向量为
法向量为![]() ,利用向量垂直数量积为零,列方程组求得
,利用向量垂直数量积为零,列方程组求得
平面![]() 法向量为
法向量为![]() ,平面
,平面![]() 的法向量,利用空间向量夹角余弦公式可得结果.
的法向量,利用空间向量夹角余弦公式可得结果.
试题解析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,
,
因为![]() 平行于
平行于![]() ,
,![]() 平行于
平行于![]() ,所以
,所以![]() 平行于
平行于![]() ,
,
所以![]() 四点共面,
四点共面,
因为![]() 平行于面
平行于面![]() ,面
,面![]() 与面
与面![]() 交与
交与![]() ,所以
,所以![]() 平行于
平行于![]() ,
,
所以![]() 为平行四边形.
为平行四边形.
所以![]() ,
,![]() .
.
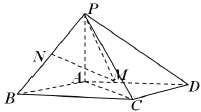
(2取![]() 中点
中点![]() ,则
,则![]() 垂直于
垂直于![]() ,因为
,因为![]() 平行于
平行于![]() ,所以
,所以![]() 垂直于
垂直于![]() ,于是以
,于是以![]() 点为原点,
点为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立坐标系,
轴建立坐标系,
由![]() 垂直于
垂直于![]() ,
,![]() 垂直于
垂直于![]() ,平面
,平面![]() 法向量为
法向量为![]() ,
,
通过计算得平面![]() 的法向量为
的法向量为![]() .经判断知二面角为钝角,于是其余弦为
.经判断知二面角为钝角,于是其余弦为![]() .
.
【方法点晴】本题主要考查线面平行的判断与性质、利用空间向量求二面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】据中国日报网报道:2017年11月13日,TOP500发布的最新一期全球超级计算机500强榜单显示,中国超算在前五名中占据两席,其中超算全球第一“神威太湖之光”完全使用了国产品牌处理器。为了了解国产品牌处理器打开文件的速度,某调查公司对两种国产品牌处理器进行了12次测试,结果如下(数值越小,速度越快,单位是MIPS)
测试1 | 测试2 | 测试3 | 测试4 | 测试5 | 测试6 | 测试7 | 测试8 | 测试9 | 测试10 | 测试11 | 测试12 | |
品牌A | 3 | 6 | 9 | 10 | 4 | 1 | 12 | 17 | 4 | 6 | 6 | 14 |
品牌B | 2 | 8 | 5 | 4 | 2 | 5 | 8 | 15 | 5 | 12 | 10 | 21 |
设![]() 分别表示第次测试中品牌A和品牌B的测试结果,记
分别表示第次测试中品牌A和品牌B的测试结果,记![]()
![]()
(Ⅰ)求数据![]() 的众数;
的众数;
(Ⅱ)从满足![]() 的测试中随机抽取两次,求品牌A的测试结果恰好有一次大于品牌B的测试结果的概率;
的测试中随机抽取两次,求品牌A的测试结果恰好有一次大于品牌B的测试结果的概率;
(Ⅲ)经过了解,前6次测试是打开含有文字和表格的文件,后6次测试是打开含有文字和图片的文件.请你依据表中数据,运用所学的统计知识,对这两种国产品牌处理器打开文件的速度进行评价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() ,
,![]() ,
,![]() 为抛物线的焦点,
为抛物线的焦点,![]() 是抛物线上两点,线段
是抛物线上两点,线段![]() 的中垂线交
的中垂线交![]() 轴于
轴于![]() ,
,![]() ,
,![]() 。
。
(Ⅰ)证明:![]() 是
是![]() 的等差中项;
的等差中项;
(Ⅱ)若![]() ,
,![]() 为平行于
为平行于![]() 轴的直线,其被以AD为直径的圆所截得的弦长为定值,求直线
轴的直线,其被以AD为直径的圆所截得的弦长为定值,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
![]()
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前,100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
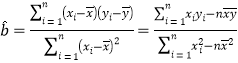 ,参考数值:
,参考数值:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() 且
且![]() ,
,![]() 是棱
是棱![]() 上的动点,
上的动点,![]() 是
是![]() 的中点.
的中点.
(1)当![]() 是
是![]() 中点时,求证:
中点时,求证:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,若存在,求
,若存在,求![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为4的菱形![]() 中,
中,![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,
的中点,![]() ,沿
,沿![]() 将
将![]() 翻折到
翻折到![]() ,连接
,连接![]() ,得到如图所示的五棱锥,且
,得到如图所示的五棱锥,且![]() .
.
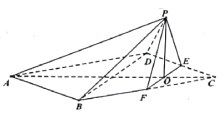
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018安徽江南十校高三3月联考】线段![]() 为圆
为圆![]() :
: ![]() 的一条直径,其端点
的一条直径,其端点![]() ,
, ![]() 在抛物线
在抛物线![]() :
: ![]() 上,且
上,且![]() ,
, ![]() 两点到抛物线
两点到抛物线![]() 焦点的距离之和为
焦点的距离之和为![]() .
.
(I)求直径![]() 所在的直线方程;
所在的直线方程;
(II)过![]() 点的直线
点的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
, ![]() 两点,抛物线
两点,抛物线![]() 在
在![]() ,
, ![]() 处的切线相交于
处的切线相交于![]() 点,求
点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
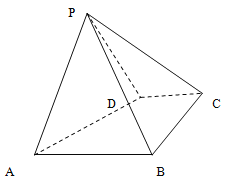
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,侧面
,侧面![]() 底面
底面![]() ,且
,且![]() 是以
是以![]() 为底的等腰三角形.
为底的等腰三角形.
(Ⅰ)证明:![]()
(Ⅱ)若四棱锥![]() 的体积等于
的体积等于![]() .问:是否存在过点
.问:是否存在过点![]() 的平面
的平面![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com