
| A. | p1,p2,p3 | B. | p2,p3 | C. | p1,p2 | D. | p1 |
分析 给出f(x)f(-x)的表达式,结合基本不等式,可判断p1,在同一坐标系中作出函数f(x)=2x-5,g(x)=4x-x2的图象,数形结合,可判断p2,p3
解答 解:∵函数f(x)=2x-5,g(x)=4x-x2,
∴f(x)f(-x)=(2x-5)(2-x-5)=26-5(2x+2-x)≤26-10$\sqrt{{2}^{x}{2}^{-x}}$=16,
故p1:若x∈R,则f(x)f(-x)的最大值为16,为真命题;
在同一坐标系中作出函数f(x)=2x-5,g(x)=4x-x2的图象如下图所示:
由图可得:p2:不等式f(x)<g(x)的解集为集合{x|-1<x<3}的真子集,为真命题;
p3:当a>0时,若?x1,x2∈[a,a+2],f(x1)≥g(x2)恒成立,则a≥3,为真命题;
故选:A
点评 本题以命题的真假判断与应用为载体,考查了函数的图象和性质,数形结合思想,基本不等式,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠ADC=45°,AD=
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠ADC=45°,AD=查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
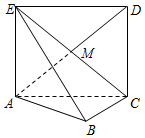 如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC=2
如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC=2查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=\frac{{(x-1)({x^4}-3{x^2})}}{x-1}$ | B. | f(x)=x3-2x | ||
| C. | $f(x)=\frac{{{x^2}+1}}{x}$ | D. | f(x)=x2+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M?N | B. | N?M | C. | M=N | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com