
分析 由题可知,f(x)=a+1-$\frac{3sinx}{h(x)}$,令g(x)=$\frac{3sinx}{h(x)}$;由于h(x)是偶函数,sinx是奇函数,故g(x)为奇函数.
由于f(x)存在最大值与最小值,则g(x)也存在最大值和最小值;g(x)为奇函数,则g(x)min+g(x)max=0
解答 解:由题可知,f(x)=a+1-$\frac{3sinx}{h(x)}$,令g(x)=$\frac{3sinx}{h(x)}$;
由于h(x)是偶函数,sinx是奇函数,故g(x)为奇函数.
由于f(x)存在最大值与最小值,则g(x)也存在最大值和最小值;
g(x)为奇函数,则g(x)min+g(x)max=0
f(x)=a+1-3g(x)
则f(x)min+f(x)max=2(a+1)-3[g(x)min+g(x)max]
由于g(x)min+g(x)max=0,M+N=8;
则有2(a+1)=8,⇒a=3.
故答案为:3
点评 本题主要考查了函数的奇偶性与对称性,函数的最值问题,属中等题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:选择题
| A. | {$-\frac{1}{2},_{\;}^{\;}\frac{1}{3}$} | B. | {$-\frac{1}{2}$} | C. | {$\frac{1}{3}$} | D. | {$0,-\frac{1}{2},\frac{1}{3}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (3,-1) | C. | (-∞,3)及(1,+∞) | D. | (-∞,-1)及(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 48 | C. | 66 | D. | 132 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
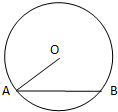
| A. | 2 | B. | 4 | ||
| C. | 8 | D. | 和动圆O的半径有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p1,p2,p3 | B. | p2,p3 | C. | p1,p2 | D. | p1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com