
【题目】已知![]() 为实数,用
为实数,用![]() 表示不超过
表示不超过![]() 的最大整数,例如
的最大整数,例如![]() ,
,![]() ,
,![]() ,对于函数
,对于函数![]() ,若存在
,若存在![]() ,
,![]() ,使得
,使得![]() ,则称函数
,则称函数![]() 是“
是“![]() 函数”.
函数”.
(1)判断函数![]() ,
,![]() 是否是“
是否是“![]() 函数”;
函数”;
(2)设函数![]() 是定义在
是定义在![]() 上的周期函数,其最小正周期是
上的周期函数,其最小正周期是![]() ,若
,若![]() 不是“
不是“![]() 函数”,求
函数”,求![]() 的最小值;
的最小值;
(3)若函数![]() 是“
是“![]() 函数”,求
函数”,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 是,
是,![]() 不是;(2)1;(3)
不是;(2)1;(3)![]() ,且
,且![]() ,
,![]() .
.
【解析】
(1)举例说明函数![]() 是
是![]() 函数,证明函数
函数,证明函数![]() 不是“
不是“![]() 函数”;
函数”;
(2)假设![]() ,得到矛盾,再证明
,得到矛盾,再证明![]() 得证;
得证;
(3)对![]() 分
分![]() 三种情况讨论得解.
三种情况讨论得解.
(1)对于函数![]() 是
是![]() 函数,设
函数,设![]() ,
,![]()
则![]() ,
,![]() ,
,
所以存在![]() ,
,![]() ,使得
,使得![]() ,所以函数
,所以函数![]() 是“
是“![]() 函数”.
函数”.
对于函数![]() ,函数的最小正周期为
,函数的最小正周期为![]() ,函数的图象如图所示,
,函数的图象如图所示,
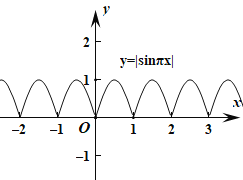
不妨研究函数在[0,1]这个周期的图象.
设![]() ,
,![]() ,则
,则![]() ,
,
所以![]() ,
,
所以函数![]() 不是“
不是“![]() 函数”.
函数”.
综合得函数![]() 是“
是“![]() 函数”,函数
函数”,函数![]() 不是“
不是“![]() 函数”.
函数”.
(2)![]() 的最小值为1.
的最小值为1.
因为![]() 是以
是以![]() 为最小正周期的周期函数,所以
为最小正周期的周期函数,所以![]() .
.
假设![]() ,则
,则![]() ,所以
,所以![]() ,矛盾.
,矛盾.
所以必有![]() .
.
而函数![]() 的周期为1,且显然不是
的周期为1,且显然不是![]() 函数,
函数,
综上所述,![]() 的最小值为1.
的最小值为1.
(3)当函数![]() 是“
是“![]() 函数”时,
函数”时,
若![]() ,则
,则![]() 显然不是
显然不是![]() 函数,矛盾.
函数,矛盾.
若![]() ,则
,则![]() ,
,
所以![]() 在
在![]() ,
,![]() 上单调递增,
上单调递增,
此时不存在![]() ,使得
,使得![]() ,
,
同理不存在![]() ,使得
,使得![]() ,
,
又注意到![]() ,即不会出现
,即不会出现![]() 的情形,
的情形,
所以此时![]() 不是
不是![]() 函数.
函数.
当![]() 时,设
时,设![]() ,所以
,所以![]() ,
,
所以有![]() ,其中
,其中![]() ,
,
当![]() 时,
时,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
综上所述,![]() ,且
,且![]() ,
,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】现从某学校中选出![]() 名学生,统计了
名学生,统计了![]() 名学生一周的户外运动时间(分钟)总和,得到如图所示的频率分布直方图和统计表格.
名学生一周的户外运动时间(分钟)总和,得到如图所示的频率分布直方图和统计表格.

(1)写出![]() 的值,并估计该学校人均每周的户外运动时间(同一组数据用该组区间的中点值作代表);
的值,并估计该学校人均每周的户外运动时间(同一组数据用该组区间的中点值作代表);
(2)从该校学生中抽取5名学生,记5名学生中每周户外运动时长在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)完成下列![]() 列联表,并回答能否有90%的把握认为“每周至少运动130分钟与性别有关”?
列联表,并回答能否有90%的把握认为“每周至少运动130分钟与性别有关”?
每周户外运动时间不少于130分钟 | 每周户外运动时间少于130分钟 | 合计 | |
男 | |||
女 | |||
合计 |
附: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离为
的距离为![]() ,若点
,若点![]() 为抛物线
为抛物线![]() 准线上的动点,给出以下命题:
准线上的动点,给出以下命题:
①当![]() 为正三角形时,
为正三角形时,![]() 的值为
的值为![]() ;
;
②存在![]() 点,使得
点,使得![]() ;
;
③若![]() ,则
,则![]() 等于
等于![]() ;
;
④![]() 的最小值为
的最小值为![]() ,则
,则![]() 等于
等于![]() 或
或![]() .
.
其中正确的是( )
A.①③④B.②③C.①③D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 的焦点为F,P为其上一动点,设直线l与抛物线C相交于A,B两点,点
的焦点为F,P为其上一动点,设直线l与抛物线C相交于A,B两点,点![]() 下列结论正确的是( )
下列结论正确的是( )
A.|PM| +|PF|的最小值为3
B.抛物线C上的动点到点![]() 的距离最小值为3
的距离最小值为3
C.存在直线l,使得A,B两点关于![]() 对称
对称
D.若过A、B的抛物线的两条切线交准线于点T,则A、B两点的纵坐标之和最小值为2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学中的数形结合也可以组成世间万物的绚丽画面,一些优美的曲线是数学形象美、对称美、和谐美的产物,曲线![]() 为四叶玫瑰线,下列结论正确的有( )
为四叶玫瑰线,下列结论正确的有( )
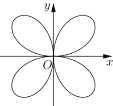
(1)方程![]() (
(![]() ),表示的曲线在第二和第四象限;
),表示的曲线在第二和第四象限;
(2)曲线![]() 上任一点到坐标原点
上任一点到坐标原点![]() 的距离都不超过2;
的距离都不超过2;
(3)曲线![]() 构成的四叶玫瑰线面积大于
构成的四叶玫瑰线面积大于![]() ;
;
(4)曲线![]() 上有5个整点(横、纵坐标均为整数的点);
上有5个整点(横、纵坐标均为整数的点);
A.(1)(2)B.(1)(2)(3)
C.(1)(2)(4)D.(1)(3)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,把
,把![]() 上各点横坐标伸长为原来的2倍,纵坐标不变,得到函数
上各点横坐标伸长为原来的2倍,纵坐标不变,得到函数![]() 的图象,关于
的图象,关于![]() 有下述四个结论:
有下述四个结论:
(1)函数![]() 在
在![]() 上是减函数;
上是减函数;
(2)当![]() ,且
,且![]() 时,
时,![]() ,则
,则![]() ;
;
(3)函数![]() (其中
(其中![]() )的最小值为
)的最小值为![]() .
.
其中正确结论的个数为( ).
A.1B.2C.3D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形![]() 为菱形,且
为菱形,且![]() ,取
,取![]() 中点为
中点为![]() .现将四边形
.现将四边形![]() 沿
沿![]() 折起至
折起至![]() ,使得
,使得![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若点![]() 满足
满足![]() ,当
,当![]() 平面
平面![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了推进分级诊疗,实现“基层首诊、双向转诊、急慢分治、上下联动”的诊疗模式,某地区自2016年起全面推行家庭医生签约服务.已知该地区居民约为2000万,从1岁到101岁的居民年龄结构的频率分布直方图如图1所示.为了解各年龄段居民签约家庭医生的情况,现调查了1000名年满18周岁的居民,各年龄段被访者签约率如图2所示.
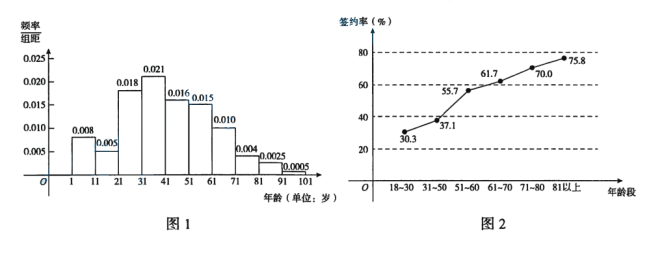
(1)估计该地区年龄在71~80岁且已签约家庭医生的居民人数;
(2)若以图2中年龄在71~80岁居民签约率作为此地区该年龄段每个居民签约家庭医生的概率,则从该地区年龄在71~80岁居民中随机抽取两人,求这两人中恰有1人已签约家庭医生的概率;
(3)据统计,该地区被访者的签约率约为![]() .为把该地区年满18周岁居民的签约率提高到
.为把该地区年满18周岁居民的签约率提高到![]() 以上,应着重提高图2中哪个年龄段的签约率?并结合数据对你的结论作出解释.
以上,应着重提高图2中哪个年龄段的签约率?并结合数据对你的结论作出解释.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】.对于n∈N*(n≥2),定义一个如下数阵: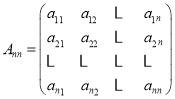 ,其中对任意的1≤i≤n,1≤j≤n,当i能整除j时,aij=1;当i不能整除j时,aij=0.设
,其中对任意的1≤i≤n,1≤j≤n,当i能整除j时,aij=1;当i不能整除j时,aij=0.设![]() .
.
(Ⅰ)当n=6时,试写出数阵A66并计算![]() ;
;
(Ⅱ)若[x]表示不超过x的最大整数,求证:![]() ;
;
(Ⅲ)若![]() ,
,![]() ,求证:g(n)﹣1<f(n)<g(n)+1.
,求证:g(n)﹣1<f(n)<g(n)+1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com