练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．双曲线$\frac{y^2}{3}-{x^2}=1$的焦点坐标是（　　）
    A．$（±\sqrt{2}，0）$B．$（0，±\sqrt{2}）$C．（0，±2）D．（±2，0）

    分析 根据题意，由双曲线的标准方程分析可得其焦点位置以及c的值，由此可得其焦点坐标．

    解答 解：根据题意，双曲线的方程为：$\frac{y^2}{3}-{x^2}=1$，
    其焦点在y轴上，且c=$\sqrt{3+1}$=2；
    则其焦点坐标为（0，±2），
    故选：C．

    点评 本题考查双曲线的几何性质，注意由双曲线的标准方程确定其焦点的位置．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    13．理科竞赛小组有9名女生、12名男生，从中随机抽取一个容量为7的样本进行分析．
    （Ⅰ）如果按照性别比例分层抽样，可以得到多少个不同的样本？（写出算式即可）
    （Ⅱ）如果随机抽取的7名同学的物理、化学成绩（单位：分）对应如表：
     学生序号 1 2 3 4 5 6 7
     物理成绩 65 70 75 81 85 87 93
     化学成绩 72 68 80 85 90 86 91
    规定85分以上（包括85份）为优秀，从这7名同学中再抽取3名同学，记这3名同学中物理和化学成绩均为优秀的人数为X，求随机变量X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．三次函数f（x）=ax3-$\frac{3}{2}$x2+2x+1的图象在点（1，f（1））处的切线与x轴平行，则实数a=（　　）
    A．$\frac{1}{3}$B．$\frac{2}{3}$C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．设抛物线K：x2=2py（p＞0），焦点为F，P是K上一点，K在点P处的切线为l，d为F到l的距离，则（　　）
    A．$\frac{d}{|PF|}$=pB．$\frac{d}{|PF{|}^{2}}$=pC．$\frac{d}{|PF|}$=2pD．$\frac{{d}^{2}}{|PF|}$=$\frac{p}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．定义[x]表示不超过x的最大整数，例如[2.11]=2，[-1.39]=-2，执行如下图所示的程序框图，则输出m的值为
    （　　）
    A．$\frac{19}{3}$B．$\frac{53}{8}$C．$\frac{171}{6}$D．$\frac{185}{8}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．某几何体的三视图如图所示，且该几何体的体积是12，则正视图中的x的值是（　　）
    A．3B．4C．9D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

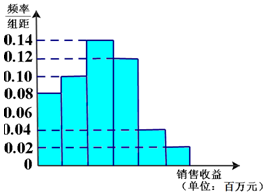    15．简阳羊肉汤已入选成都市级非遗项目，成为简阳的名片．当初向各地作了广告推广，同时广告对销售收益也有影响．在若干地区各投入4万元广告费用，并将各地的销售收益绘制成频率分布直方图（如图所示）．由于工作人员操作失误，横轴的数据丢失，但可以确定横轴是从0开始计数的．
    （Ⅰ）根据频率分布直方图，计算图中各小长方形的宽度；
    （Ⅱ）根据频率分布直方图，估计投入4万元广告费用之后，销售收益的平均值（以各组的区间中点值代表该组的取值）；
    （Ⅲ）按照类似的研究方法，测得另外一些数据，并整理得到下表：
    广告投入x（单位：万元）12345
    销售收益y（单位：百万元）2327
    表中的数据显示，x与y之间存在线性相关关系，请将（Ⅱ）的结果填入空白栏，并计算y关于x的回归方程．回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．若集合A={x|x（x-3）≤0，x∈N}，B={-1，0，1}，则集合A∩B为（　　）
    A．{-1，0}B．{1}C．{0，1}D．{-1，0，1，2，3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知i是虚数单位，若复数z=$\frac{3+4i}{i}$，则z的共轭复数$\overline{z}$的虚部为（　　）
    A．-3iB．-3C．3iD．3

    查看答案和解析>>

    同步练习册答案