
| A. | $\frac{7}{3}$ | B. | $\frac{11}{3}$ | C. | $\frac{7}{2}$ | D. | $\frac{9}{2}$ |
分析 根据条件,可分别以CB,CA为x轴,y轴,建立平面直角坐标系,然后可求出C,A,B,E,F,D这几点的坐标,从而可分别求出直线AD,CE,CF的方程,联立方程即可分别求出点G,H的坐标,进而求出向量$\overrightarrow{CG},\overrightarrow{CH}$的坐标,从而求出该数量积的值.
解答 解:如图,分别以CB,CA为x,y轴,建立平面直角坐标系,则: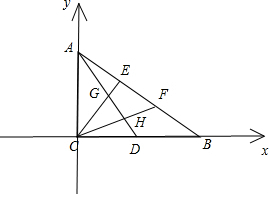 C(0,0),A(0,3),B(6,0),E(2,2),F(4,1),D(3,0);
C(0,0),A(0,3),B(6,0),E(2,2),F(4,1),D(3,0);
∴${k}_{AD}=-1,{k}_{CE}=1,{k}_{CF}=\frac{1}{4}$;
∴直线AD的方程为y-3=-x,即y=3-x;
直线CE:y=x,直线CF:y=$\frac{1}{4}x$;
解$\left\{\begin{array}{l}{y=3-x}\\{y=x}\end{array}\right.$得,$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=\frac{3}{2}}\end{array}\right.$,G($\frac{3}{2}$,$\frac{3}{2}$);
解$\left\{\begin{array}{l}{y=3-x}\\{y=\frac{1}{4}x}\end{array}\right.$得,$\left\{\begin{array}{l}{x=\frac{12}{5}}\\{y=\frac{3}{5}}\end{array}\right.$,$H(\frac{12}{5},\frac{3}{5})$;
∴$\overrightarrow{CG}•\overrightarrow{CH}=(\frac{3}{2},\frac{3}{2})•(\frac{12}{5},\frac{3}{5})=\frac{18}{5}+\frac{9}{10}$=$\frac{9}{2}$.
故选D.
点评 考查通过建立平面直角坐标系,利用坐标解决向量问题的方法,能求平面上点的坐标,根据点的坐标可求过两点的直线方程,根据直线方程可求直线的交点坐标,以及向量数量积的坐标运算.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | -4 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{64}$ | B. | -$\frac{1}{64}$ | C. | $\frac{1}{32}$ | D. | -$\frac{1}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com