练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知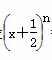的展开式中前三项的系数成等差数列．设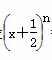＝a0＋a1x＋a2x2＋…＋anxn.求：

    (1) a5的值；

    (2) a0－a1＋a2－a3＋…＋(－1)nan的值；

    (3) ai(i＝0，1，2，…，n)的最大值．


    解：(1) 由题设，得

    即n2－9n＋8＝0，解得n＝8，n＝1(舍)．

    Tr＋1＝Cx8－r，

    令8－r＝5r＝3，所以a5＝7.

    (2) 在等式的两边取x＝－1，得a0－a1＋a2－a3＋…＋a8＝ .

    (3) 设第r＋1的系数最大，则

    即解得r＝2或r＝3.

    所以ai系数最大值为7.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设P(x，y)为函数y＝x2－1(x＞)图象上一动点，记m＝，则当m最小时，点P的坐标为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某班级有男生5人，女生4人，从中任选一人去领奖，有________种不同的选法．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    现有5位同学准备一起做一项游戏，他们的身高各不相同．现在要从他们5个人当中选择出若干人组成A、B两个小组，每个小组都至少有1人，并且要求B组中最矮的那个同学的身高要比A组中最高的那个同学还要高．则不同的选法共有______种．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如果的展开式中，第四项和第七项的二项式系数相等，求：

    (1) 展开式的中间项；

    (2) 展开式中所有的有理项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     (1＋x)3(1＋y)4的展开式中x2y2的系数是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列问题属于超几何分布的有________．(填序号)

    ① 抛掷三枚骰子，所得向上的数是6的骰子的个数记为X，求X的概率分布列；

    ② 有一批种子的发芽率为70%，现任取10颗种子做发芽实验，把实验中发芽的种子的个数记为X，求X的概率分布列；

    ③ 一盒子中有红球3只，黄球4只，蓝球5只，现任取3只球，把不是红色的球的个数记为X，求X的概率分布列；

    ④ 某班级有男生25人，女生20人，现选派4名学生参加学校组织的活动，班长必须参加，其中女生人数记为X，求X的概率分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    袋中装有黑球和白球共7个，从中任取2个球都是白球的概率为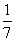，现有甲、乙两人从袋中轮流摸取1球，甲先取，乙后取，然后甲再取，…，取后不放回，直到两人中有一人取到白球时即终止，每个球在每一次被取出的机会是等可能的，用ξ表示取球终止所需要的取球次数．

    (1) 求袋中原有白球的个数；

    (2) 求随机变量ξ的概率分布；

    (3) 求甲取到白球的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，＝________．(用b、c表示)

    查看答案和解析>>

    同步练习册答案