
现有5位同学准备一起做一项游戏,他们的身高各不相同.现在要从他们5个人当中选择出若干人组成A、B两个小组,每个小组都至少有1人,并且要求B组中最矮的那个同学的身高要比A组中最高的那个同学还要高.则不同的选法共有______种.
49
解析:给5位同学按身高的不同由矮到高分别编号为1,2,3,4,5,组成集合M={1,2,3,4,5}.
① 若小组A中最高者为1,则能使B中最矮者高于A中最高者的小组B是{2,3,4,5}的非空子集,这样的子集有C +C
+C +C
+C +C
+C =24-1=15个,∴ 不同的选法有15个;②若A中最高者为2,则这样的小组A有2个:{2}、{1,2},能使B中最矮者高于A中最高者的小组B是{3,4,5}的非空子集,这样的子集(小组B)有23-1=7个,∴ 不同的选法有2×7=14个;③若A中最高者为3,则这样的小组A有4个:{3}、{1,3}、{2,3}、{1,2,3},能使B中最矮者高于A中最高者的小组B是{4,5}的非空子集,这样的子集(小组B)有22-1=3个,∴ 不同的选法有4×3=12个;④若A中最高者为4,则这样的小组A有8个:{4}、{1,4}、{2,4}、{3,4}、{1,2,4}、{1,3,4}、{2,3,4}、{1,2,3,4},能使B中最矮者高于A中最高者的小组B只有{5} 1个,∴ 不同的选法有8个.∴ 综上,所有不同的选法是15+14+12+8=49个.
=24-1=15个,∴ 不同的选法有15个;②若A中最高者为2,则这样的小组A有2个:{2}、{1,2},能使B中最矮者高于A中最高者的小组B是{3,4,5}的非空子集,这样的子集(小组B)有23-1=7个,∴ 不同的选法有2×7=14个;③若A中最高者为3,则这样的小组A有4个:{3}、{1,3}、{2,3}、{1,2,3},能使B中最矮者高于A中最高者的小组B是{4,5}的非空子集,这样的子集(小组B)有22-1=3个,∴ 不同的选法有4×3=12个;④若A中最高者为4,则这样的小组A有8个:{4}、{1,4}、{2,4}、{3,4}、{1,2,4}、{1,3,4}、{2,3,4}、{1,2,3,4},能使B中最矮者高于A中最高者的小组B只有{5} 1个,∴ 不同的选法有8个.∴ 综上,所有不同的选法是15+14+12+8=49个.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
已知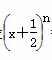 的展开式中前三项的系数成等差数列.设
的展开式中前三项的系数成等差数列.设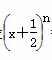 =a0+a1x+a2x2+…+anxn.求:
=a0+a1x+a2x2+…+anxn.求:
(1) a5的值;
(2) a0-a1+a2-a3+…+(-1)nan的值;
(3) ai(i=0,1,2,…,n)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
随机地将编号为1,2,3的三个小球放入编号为1,2,3的三个盒子中,每个盒子放入一个小球,当球的编号与盒子的编号相同时叫做“放对球”,否则叫做“放错球”,设放对球的个数为ξ.求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
一盒中装有零件12个,其中有9个正品,3个次品,从中任取一个,如果每次取出次品就不再放回去,再取一个零件,直到取得正品为止.求在取得正品之前已取出次品数的期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com