
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:解答题
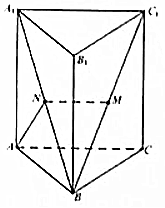 如图,直三棱柱ABC-A1B1C1中,AA1=AB,AB⊥BC,且N是A1B的中点.
如图,直三棱柱ABC-A1B1C1中,AA1=AB,AB⊥BC,且N是A1B的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “?x∈R,ex>0”的否定是“?x∈R,使ex>0” | |
| B. | 若x+y≠3(x,y∈R),则x≠2或y≠1 | |
| C. | “x2+2x≥ax(1≤x≤2)恒成立”等价于“(x2+2x)min≥(ax)max(1≤x≤2)” | |
| D. | “若a=-1,则函数f(x)=ax2+2x-1只有一个零点”的逆命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{25}$ | B. | $-\frac{12}{25}$ | C. | $\frac{24}{25}$ | D. | $-\frac{24}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 10 | 20 | 30 | 40 | 50 |
| y | 62 | a | 75 | 81 | 89 |
| A. | 68 | B. | 70 | C. | 75 | D. | 72 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
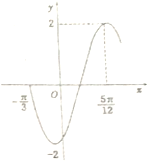 函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为( )
函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为( )| A. | y=2sin(2x-$\frac{π}{6}$) | B. | y=2sin(2x+$\frac{π}{6}$) | C. | y=2sin(2x) | D. | y=2sin(2x+$\frac{π}{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com