
分析 (1)通过9an+1an-2•an+1-4an+1=0可知an+1=$\frac{4{a}_{n}-1}{9{a}_{n}-2}$,进而利用a1=1直接代入计算即得结论;
(2)通过(1)可猜想an=$\frac{2n-1}{6n-5}$,进而利用数学归纳法证明即可.
解答 解:(1)∵9an+1an-2•an+1-4an+1=0,
∴an+1=$\frac{4{a}_{n}-1}{9{a}_{n}-2}$,
又∵a1=1,
∴a2=$\frac{3}{7}$,a3=$\frac{5}{13}$,a4=$\frac{7}{19}$;
(2)由(1)可猜想an=$\frac{2n-1}{6n-5}$.
下面用数学归纳法来证明:
①当n=1时,a1=1结论显然成立;
②假设当n=k时(k∈N+)时,结论成立,即ak=$\frac{2k-1}{6k-5}$,
则当n=k+1时,有ak+1=$\frac{4{a}_{k}-1}{9{a}_{k}-2}$=$\frac{4•\frac{2k-1}{6k-5}-1}{9•\frac{2k-1}{6k-5}-2}$=$\frac{2k+1}{6k+1}$=$\frac{2(k+1)-1}{6(k+1)-5}$,
即当n=k+1时命题也成立;
由①②可知an=$\frac{2n-1}{6n-5}$.
点评 本题考查数列的通项及前n项和,考查数学归纳法,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:填空题
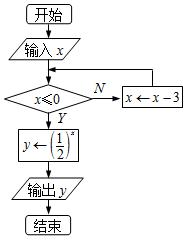 如图,是一个算法的程序框图,当输出的y值为2时,若将输入的x的所有可能值按从小到大的顺序排列得到一个数列{an},则该数列的通项公式为an=an=3n-4.
如图,是一个算法的程序框图,当输出的y值为2时,若将输入的x的所有可能值按从小到大的顺序排列得到一个数列{an},则该数列的通项公式为an=an=3n-4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 为了了解某火车站候车旅客用手机使用火车站WIFI情况,在某日15:00时,把该候车厅10至50岁年龄段的旅客按年龄分区间[10,20),[20,30),[30,40),[40,50]得到如图所示的人数频率分布直方图,现用分层抽样的方法从中得到一样本.若样本在区间[20,30)上有6人,则该样本在区间[40,50]上有4人.
为了了解某火车站候车旅客用手机使用火车站WIFI情况,在某日15:00时,把该候车厅10至50岁年龄段的旅客按年龄分区间[10,20),[20,30),[30,40),[40,50]得到如图所示的人数频率分布直方图,现用分层抽样的方法从中得到一样本.若样本在区间[20,30)上有6人,则该样本在区间[40,50]上有4人.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8+4π | B. | 4+4π | C. | 8+2π | D. | 4+2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,16) | B. | (0,12) | C. | (9,21) | D. | (15,25) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com