
 为了了解某火车站候车旅客用手机使用火车站WIFI情况,在某日15:00时,把该候车厅10至50岁年龄段的旅客按年龄分区间[10,20),[20,30),[30,40),[40,50]得到如图所示的人数频率分布直方图,现用分层抽样的方法从中得到一样本.若样本在区间[20,30)上有6人,则该样本在区间[40,50]上有4人.
为了了解某火车站候车旅客用手机使用火车站WIFI情况,在某日15:00时,把该候车厅10至50岁年龄段的旅客按年龄分区间[10,20),[20,30),[30,40),[40,50]得到如图所示的人数频率分布直方图,现用分层抽样的方法从中得到一样本.若样本在区间[20,30)上有6人,则该样本在区间[40,50]上有4人.  快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 27种 | B. | 48种 | C. | 54种 | D. | 72种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
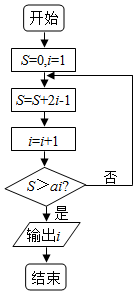
| A. | ?a∈(2,4),输出的i的值为5 | B. | ?a∈(4,5),输出的i的值为5 | ||
| C. | ?a∈(3,4),输出的i的值为5 | D. | ?a∈(2,4),输出的i的值为5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
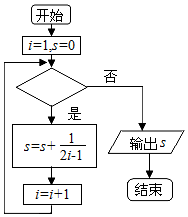
| A. | i≤1008? | B. | i>1008? | C. | i≤1009? | D. | i>1009? |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com