
分析 ①对于任意λ∈R,f(x)=0时,f(x+λ)+λf(x)=0对任意的实数x都成立,从而判断;
②假设f(x)=x2是一个λ一伴随函数;从而推出矛盾即可,从而判断;
③假设f(x)=2x是一个λ一伴随函数;从而可推出2λ+λ=0;结合方程的根与函数的零点的关系可判断方程有解,从而判断;
④若f(x)是$\frac{1}{2}$一伴随函数;从而可得f(x+$\frac{1}{2}$)+$\frac{1}{2}$f(x)=0,再利用函数零点的判定定理判断即可.
解答 解:①对于任意λ∈R,f(x)=0时,f(x+λ)+λf(x)=0对任意的实数x都成立,
故可判断f(x)=0是唯一的一个对任意λ都成立的λ一伴随函数;
故①不正确;
②若f(x)=x2是一个λ一伴随函数;
则存在常数λ(λ∈R),
使f(x+λ)+λf(x)=0恒成立,
即(x+λ)2+λx2=0;
当x=0时,λ=0;
当x≠0,λ=0时,(x+λ)2+λx2=0不成立;
故②不正确;
③若f(x)=2x是一个λ一伴随函数;
则存在常数λ(λ∈R),
使f(x+λ)+λf(x)=0恒成立,
即2x+λ+λ2x=0;
即2x(2λ+λ)=0,
即2λ+λ=0;
由方程的根与函数的零点的关系知,
存在λ0,使2λ+λ=0成立;
故③正确;
④若f(x)是$\frac{1}{2}$一伴随函数;
则f(x+$\frac{1}{2}$)+$\frac{1}{2}$f(x)=0,
若f(x)=0,则f(x+$\frac{1}{2}$)=0,
则x,x+$\frac{1}{2}$是f(x)的零点;
若f(x)≠0,则f(x)•f(x+$\frac{1}{2}$)<0,
则f(x)在(x,x$+\frac{1}{2}$)上有零点;
故④正确;
故答案为:①②.
点评 本题考查了学生对新定义的接受与应用能力,同时考查了函数零点的判断与应用,属于中档题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
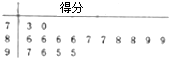 钓鱼岛及其附近海域自古以来就是中国人民进行捕鱼、避风、休息的场所,被誉为深海中的翡翠.某学校就钓鱼岛有关常识随机抽取了16名学生进行测试,用“10分制”以茎叶图方式记录了他们对钓鱼岛的了解程度,分数以小数点前的一位数字为茎,小数点后的一位数字为叶.
钓鱼岛及其附近海域自古以来就是中国人民进行捕鱼、避风、休息的场所,被誉为深海中的翡翠.某学校就钓鱼岛有关常识随机抽取了16名学生进行测试,用“10分制”以茎叶图方式记录了他们对钓鱼岛的了解程度,分数以小数点前的一位数字为茎,小数点后的一位数字为叶.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com