
分析 (1)由焦点坐标可求得c,代入点求出椭圆方程.
(2)直线$y-\frac{\sqrt{2}}{2}=k(x-1)$,与抛物线相交根据条件列式求解即可.
解答 解:(1)设椭圆C1的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,依题意得:$\left\{\begin{array}{l}{\frac{{1}^{2}}{{a}^{2}}+\frac{(\frac{\sqrt{2}}{2})^{2}}{{b}^{2}}=1}\\{{a}^{2}={b}^{2}+1}\end{array}\right.$
解得:a2=2,b2=1,所以椭圆方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$
(2)当过点A的直线L斜率不存在时,直线L与抛物线x2=4y只有一个交点,不合题意
故可设过点A的直线为$y-\frac{\sqrt{2}}{2}=k(x-1)$,与抛物线的交点为B(x1,y1),C(x2,y2)
由$\left\{\begin{array}{l}{y-\frac{\sqrt{2}}{2}=k(x-1)}\\{{x}^{2}=4y}\end{array}\right.$得,x2-4kx+4k-2$\sqrt{2}$=0,
△=16k2-16k+8$\sqrt{2}$=16(x-$\frac{1}{2}$)2-4+8$\sqrt{2}$>0恒成立.
∴x1+x2=4k,x1x2=4k-2$\sqrt{2}$①
由x2=4y,即y=$\frac{1}{4}{x}^{2}$,得y'=$\frac{1}{2}x$
∴抛物线C2在点C处的切线l2的方程为$y-\frac{1}{4}{x}_{1}^{2}=\frac{{x}_{1}}{2}(x-{x}_{1})$即$y=\frac{{x}_{1}}{2}x-\frac{1}{4}{x}_{1}^{2}②$
同理,抛物线C2在点B处切线l2的方程为$y=\frac{{x}_{2}}{2}x-\frac{1}{4}{x}_{2}^{2}③$
设l1与l2交点P(x,y)由②③解得:$\frac{{x}_{1}}{2}x-\frac{1}{4}{x}_{1}^{2}=\frac{{x}_{2}}{2}x-\frac{1}{4}{x}_{2}^{2}$
而x1≠x2,则x=$\frac{1}{2}({x}_{1}+{x}_{2})$,代入②得y=$\frac{1}{4}{x}_{1}{x}_{2}$
由①得点P的坐标为($2k,k-\frac{\sqrt{2}}{2}$)
由$|\overrightarrow{{PF}_{1}}|$$+|\overrightarrow{P{F}_{2}}|=|\overrightarrow{A{F}_{1}}|+|\overrightarrow{A{F}_{2}}|$,得点P在椭圆C1上,代入椭圆方程,得,
$\frac{4{k}^{2}}{2}+(k-\frac{\sqrt{2}}{2})^{2}=1$,即3k2-$\sqrt{2}$k-$\frac{1}{2}=0$
∵△=2-4×3×$(-\frac{1}{2})^{2}>0$,方程有2解.
所以满足条件的点P有2个.
点评 本题主要考查了抛物线方程的求法和直线与圆锥曲线的综合问题,属常考题型,中档题目.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 3 | C. | 11 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
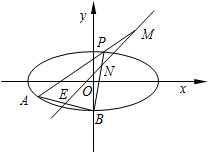 如图,已知椭圆$C:\frac{x^2}{12}+\frac{y^2}{4}=1$,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在x轴下方),且线段AB的中点E在直线y=x上.
如图,已知椭圆$C:\frac{x^2}{12}+\frac{y^2}{4}=1$,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在x轴下方),且线段AB的中点E在直线y=x上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 双曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9}$=1与椭圆$\frac{{x}^{2}}{35}$+y2=1有相同的焦点 | |
| B. | “0<x<2”是“x2-2x-3<0”充分不必要条件 | |
| C. | “若xy=0,则x、y中至少有一个为0”的否命题是真命题. | |
| D. | “?x∈R,使x2-2x+3≤0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com