
| A. | 双曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9}$=1与椭圆$\frac{{x}^{2}}{35}$+y2=1有相同的焦点 | |
| B. | “0<x<2”是“x2-2x-3<0”充分不必要条件 | |
| C. | “若xy=0,则x、y中至少有一个为0”的否命题是真命题. | |
| D. | “?x∈R,使x2-2x+3≤0” |
分析 可选用排除法,或者四个选项先找最容易解决的,其实D项是很简单的一个命题,如果能看到这一点,这一题便很容易解决.
解答 解:对于A项,双曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9}$=1的焦点为($\sqrt{34},0$)和($-\sqrt{34},0$).椭圆$\frac{{x}^{2}}{35}$+y2=1的焦点为($\sqrt{34},0$)和($-\sqrt{34},0$).所以A选项为真命题.
对于B项,x2-2x-3<0的解集为{x|-1<x<3},{x|0<x<2}⊆{x|-1<x<3},∴“0<x<2”是“x2-2x-3<0”充分不必要条件,B选项为真命题.
对于C项,“若xy=0,则x、y中至少有一个为0”的否命题是““若xy≠0,则x、y中没有一个为0”为真命题,C选项为真命题.
对于D项,x2-2x+3=(x-1)2+2>0.所以不存在这样的x使得式子成立.故D项为假命题.
故选:D.
点评 本题考查了逻辑用语的基础知识,知识面广,考查力度大,是高考常考题型.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
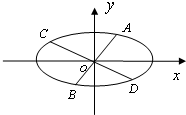 椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条直线段,称为该直径的共轭直径.已知椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1
椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条直线段,称为该直径的共轭直径.已知椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com