练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．设F1、F2分别是椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的左、焦点，P为椭圆上一点，M是F1P的中点，|OM|=3，则P点到椭圆左焦点的距离为（　　）
    A．2B．3C．4D．5

    分析 由题意知，OM是三角形PF1F2的中位线，由|OM|=3，可得|PF2|=6，再由椭圆的定义求出|PF1|的值．

    解答 解：如图，

    则OM是三角形PF1F2的中位线，
    ∵|OM|=3，∴|PF2|=6，
    又|PF1|+|PF2|=2a=10，
    ∴|PF1|=4，
    故选：C．

    点评 本题考查椭圆的定义，以及椭圆的简单性质的应用，判断OM是三角形PF1F2的中位线是解题的关键，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    5．已知椭圆C1的中心在坐标原点，两个焦点分别为F1（-1，0），F2（1，0），点A（1，$\frac{\sqrt{2}}{2}$）在椭圆C1上，过点A的直线L与抛物线C2：x2=4y交于B，C两点，抛物线C2在点B，C处的切线分别为l1，l2，且l1与l2交于点P．
    （1）求椭圆C1的方程；
    （2）是否存在满足|$\overrightarrow{P{F}_{1}}$|$+|\overrightarrow{P{F}_{2}}|$=|$\overrightarrow{A{F}_{1}}$|$+|\overrightarrow{A{F}_{2}}|$的点P，若存在，指出这样的点P有几个（不必求出点P的坐标）；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知函数f（x）=ax2+bx+1（a，b为实数），设F（x）=$\left\{\begin{array}{l}{f（x），x＞0}\\{-f（x），x＜0}\end{array}\right.$，若f（-1）=0，且对任意实数x均有f（x）≥0成立，求F（x）的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．集合M={x|x2-2x-3＜0}，N={x|x2+x+1＞0}，则M∩N是（　　）
    A．（-3，1）B．RC．（-1，3）D．∅

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．若正数a，b满足$\frac{1}{a}$+$\frac{1}{b}$=1，则$\frac{1}{a-1}$+$\frac{4}{b-1}$的最小值为（　　）
    A．3B．4C．5D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）=ln（1+ax）-ax，（其中a为实数，且a≠0）．
    （1）求函数f（x）的单调区间；
    （2）关于x方程f（x）-a=0在[-1，1]上是否有两个不等实根？若有，求实数a的取值范围；若没有，请说明理由；
    （3）若数列{an}满足：a1=1，an+1=（1+$\frac{1}{{n}^{2}+n}$）an+$\frac{1}{{2}^{n}}$，n∈N*，证明：对于任意的正整数n，都有an＜e2，其中无理数e=2.71828．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

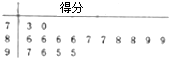    7．钓鱼岛及其附近海域自古以来就是中国人民进行捕鱼、避风、休息的场所，被誉为深海中的翡翠．某学校就钓鱼岛有关常识随机抽取了16名学生进行测试，用“10分制”以茎叶图方式记录了他们对钓鱼岛的了解程度，分数以小数点前的一位数字为茎，小数点后的一位数字为叶．
    （1）指出这组数据的众数和中位数；
    （2）若所得分数不低于9.5分，则称该学生对钓鱼岛“非常了解”．求从这16人中随机选取3人，求至多有1人“非常了解”的概率；
    （3）以这16人的样本数据来估计该所学校学生的总体数据，若从该所学校（人数可视为很多）任选3人，记ξ表示抽到“非常了解”的人数，求ξ的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．国务院召开青少年校园足球工作电视电话会议，提出教育部将主导校园足球“足球进校园”活动．某市教育部门未了解学生喜欢足球是否与性别有关，在某学校该校50名学生进行了问卷调查，得到了如下的列联表：
     喜欢足球不喜欢足球合计
    男生20525
    女生101525
    合计302050
    （Ⅰ）按性别用分层抽样的方法在喜欢足球的学生中抽取6人，求这6人中男生的人数；
    （Ⅱ）在上述抽取的6人中随机抽取2人做进一步调查，求恰有1名女生的概率；
    （Ⅲ）根据列联表的独立性检验，能否在犯错误的概率不超过0.01的前提下，认为喜欢足球与性别有关系？
    下面的临界值表供参考：
     P（K2≥k）0.150.100.050.0250.0100.0050.001
    K2.0722.7063.8415.0246.6357.87910.828
    （参考公式：${K}^{2}=\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）上为减函数，若$f（{ln\frac{n}{m}}）$+$f（{ln\frac{m}{n}}）$-2f（1）＞0，则$\frac{{{m^2}+{n^2}}}{mn}$的取值范围是（　　）
    A．（e，+∞）B．[2，e）C．$（{e+\frac{1}{e}，+∞}）$D．$[{2，e+\frac{1}{e}}）$

    查看答案和解析>>

    同步练习册答案