
分析 分类讨论:当要求的直线与MN平行时,当要求的直线经过线段MN的中点P$(0,-\frac{3}{2})$时,即可得出.
解答 解:①当要求的直线与MN平行时,kMN=$\frac{-5-2}{-1-1}$=$\frac{7}{2}$,可得直线方程为:y+3=$\frac{7}{2}$(x-2),化为:7x-2y-20=0.
②当要求的直线经过线段MN的中点P$(0,-\frac{3}{2})$时,kPC=$\frac{-3-(-\frac{3}{2})}{2-0}$=-$\frac{3}{4}$,可得直线方程为:y+3=-$\frac{3}{4}$(x-2),化为:3x+4y+6=0.
故答案为:7x-2y-20=0或3x+4y+6=0.
点评 本题考查了相互平行的直线斜率之间的关系、中点坐标公式、直线方程,考查了分类讨论方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
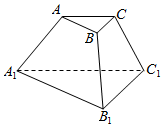
| A. | 与直线BC和直线A1B1都平行 | B. | 与直线BC和直线A1B1都垂直 | ||
| C. | 与直线BC平行且直线A1B1垂直 | D. | 与直线BC和直线A1B1所成角相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2:3 | B. | 3:4 | C. | 3:5 | D. | 4:5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com