
分析 (Ⅰ)由题意可得关于a,b的方程组,求解方程组得到a,b的值,则椭圆方程可求;
(Ⅱ)当直线AB斜率不存在时,直接求出|AB|=$3\sqrt{3}$,C到直线AB的距离d=$3\sqrt{3}$,可得△ABC的面积;当直线AB的斜率存在时,设直线AB方程为:y=kx+m,A(x1,y1),B(x2,y2).联立直线方程与椭圆方程,化为关于x的一元二次方程,由判别式大于0可得k与m的关系,利用根与系数的关系可得A,B横坐标的和与积,由O为△ABC的重心求得C的坐标把C点坐标代入椭圆方程,可得4m2=12k2+9.由弦长公式求得|AB|,再求出点C到直线AB的距离d,代入三角形面积公式整理得答案.
解答 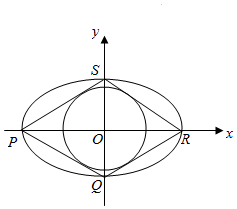 解:(Ⅰ)∵四边形PQRS是圆C0外切平行四边形,∴$\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}=\frac{6}{\sqrt{7}}$,
解:(Ⅰ)∵四边形PQRS是圆C0外切平行四边形,∴$\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}=\frac{6}{\sqrt{7}}$,
又四边形PQRS的面积S=$\frac{1}{2}×2a×2b=12\sqrt{3}$,联立解得a2=12,b2=9,
故所求椭圆C1 的方程为$\frac{{x}^{2}}{12}+\frac{{y}^{2}}{9}=1$;
(Ⅱ)当直线AB斜率不存在时,
∵O为△ABC的重心,∴C为椭圆的左、右顶点,
不妨设C($-2\sqrt{3}$,0),则直线AB的方程为x=$\sqrt{3}$,
可得|AB|=$3\sqrt{3}$,C到直线AB的距离d=$3\sqrt{3}$,
∴${S}_{△ABC}=\frac{1}{2}|AB|d$=$\frac{27}{2}$.
当直线AB的斜率存在时,设直线AB方程为:y=kx+m,
A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{12}+\frac{{y}^{2}}{9}=1}\end{array}\right.$,得(3+4k2)x2+8kmx+4m2-36=0,
则△=64k2m2-4(3+4k2)(4m2-36)=48(12k2+9-m2)>0.
即12k2+9>m2,
${x}_{1}+{x}_{2}=\frac{-8km}{3+4{k}^{2}}$,${x}_{1}{x}_{2}=\frac{4{m}^{2}-36}{3+4{k}^{2}}$,
∴${y}_{1}+{y}_{2}=k({x}_{1}+{x}_{2})+2m=\frac{6m}{3+4{k}^{2}}$.
∵O为△ABC的重心,∴$\overrightarrow{OC}=-(\overrightarrow{OA}+\overrightarrow{OB})=(\frac{8km}{3+4{k}^{2}},\frac{-6m}{3+4{k}^{2}})$,
∵C点在椭圆C1上,故有$\frac{(\frac{8km}{3+4{k}^{2}})^{2}}{12}+\frac{(\frac{-6m}{3+4{k}^{2}})^{2}}{9}=1$,
化简得4m2=12k2+9.
∴$|AB|=\sqrt{1+{k}^{2}}\sqrt{(\frac{8km}{3+4{k}^{2}})^{2}-4(\frac{4{m}^{2}-36}{3+4{k}^{2}})}$=$\frac{4\sqrt{3}•\sqrt{1+{k}^{2}}}{3+4{k}^{2}}\sqrt{12{k}^{2}+9-{m}^{2}}$.
又点C到直线AB的距离d=$\frac{|3m|}{\sqrt{1+{k}^{2}}}$(d是原点到AB距离的3倍得到).
∴${S}_{△ABC}=\frac{1}{2}|AB|•d=\frac{6\sqrt{3}|m|}{3+4{k}^{2}}\sqrt{12{k}^{2}+9-{m}^{2}}$=$\frac{6\sqrt{3}×\sqrt{3}{m}^{2}}{\frac{4}{3}{m}^{2}}=\frac{27}{2}$.
综上可得,△ABC的面积为定值$\frac{27}{2}$.
点评 本题考查椭圆的简单性质,考查直线与椭圆位置关系的应用,考查“分类讨论”的数学思想方法与“设而不求”的解题思想方法,是中档题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知四棱台ABCD-A1B1C1D1的下底面是边长为4的正方形,AA1=4,且AA1⊥面ABCD,点P为DD1的中点,点Q在BC上,BQ=3QC,DD1与面ABCD所成角的正切值为2.
已知四棱台ABCD-A1B1C1D1的下底面是边长为4的正方形,AA1=4,且AA1⊥面ABCD,点P为DD1的中点,点Q在BC上,BQ=3QC,DD1与面ABCD所成角的正切值为2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图.四棱锥P-ABCD中.平而PAD⊥平而ABCD,底而ABCD为梯形.AB∥CD,AB=
如图.四棱锥P-ABCD中.平而PAD⊥平而ABCD,底而ABCD为梯形.AB∥CD,AB=查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3600 | B. | 1080 | C. | 1440 | D. | 2520 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
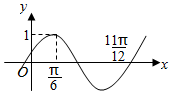 函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的图象如图所示,将f(x)的图象向右平移m个单位得到g(x)的图象关于y轴对称,则正数m的最小值为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的图象如图所示,将f(x)的图象向右平移m个单位得到g(x)的图象关于y轴对称,则正数m的最小值为( )| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com