
如图,ABCD是边长为2的正方形,ED⊥平面ABCD, ED="1," EF//BD且2EF=BD.
(1)求证:平面EAC⊥平面BDEF;
(2)求几何体ABCDEF的体积.
(1)要证明平面EAC⊥平面BDEF垂直,关键是证明AC⊥平面BDEF
(2)2
解析试题分析:(1)∵ ED⊥平面ABCD,AC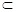 平面ABCD,
平面ABCD,
∴ ED⊥AC.
∵ ABCD是正方形,
∴ BD⊥AC,
∴ AC⊥平面BDEF.
又AC?平面EAC,故平面EAC⊥平面BDEF.
(2)连结FO,∵ EF
 DO,
DO,
∴ 四边形EFOD是平行四边形.
由ED⊥平面ABCD可得ED⊥DO,
∴ 四边形EFOD是矩形.
∵ 平面EAC⊥平面BDEF.
∴ 点F到平面ACE的距离等于就是Rt△EFO斜边EO上的高,
且高h=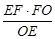 =
=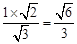 .
.
∴几何体ABCDEF的体积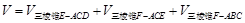
=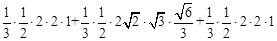
=2.
考点:面面垂直,棱锥的体积
点评:主要是考查了体积公式以及面面垂直的证明,属于基础题。


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:解答题
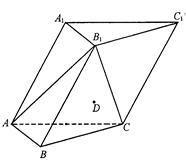
如图,在各棱长均为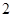 的三棱柱
的三棱柱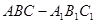 中,侧面
中,侧面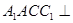 底面
底面 ,
,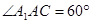 .
.
(1)求侧棱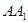 与平面
与平面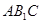 所成角的正弦值的大小;
所成角的正弦值的大小;
(2)已知点 满足
满足 ,在直线
,在直线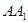 上是否存在点
上是否存在点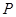 ,使
,使 ?若存在,请确定点
?若存在,请确定点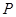 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在长方体ABCD-A1B1C1D1中,AB=2,AD=1,A1A=1,证明直线BC1平行于平面DA1C,并求直线BC1到平面D1AC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,四边形ABCD是矩形, ,F为CE上的点,且BF
,F为CE上的点,且BF 平面ACE,AC与BD交于点G
平面ACE,AC与BD交于点G
(1)求证:AE 平面BCE
平面BCE
(2)求证:AE//平面BFD
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱锥P-ABCD中,PA⊥平面ABCD, AB//CD,∠DAB=90°,PA=AD=DC=1,AB=2,M为PB的中点.
(I)证明:MC//平面PAD;
(II)求直线MC与平面PAC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在正方体ABCD—A1B1C1D1中,E、F分别为棱BB1和DD1的中点. 
(1)求证:平面B1FC//平面ADE;
(2)试在棱DC上取一点M,使 平面ADE;
平面ADE;
(3)设正方体的棱长为1,求四面体A1—FEA的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在斜三棱柱ABC—A1B1C1中,AB⊥侧面BB1C1C,BC=2,BB1=4,AB= ,∠BCC1=60°.
,∠BCC1=60°.
(Ⅰ)求证:C1B⊥平面A1B1C1;
(Ⅱ)求A1B与平面ABC所成角的正切值;
(Ⅲ)若E为CC1中点,求二面角A—EB1—A1的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com