
分析 利用“立方和公式”、倍角公式、和差化积即可得出.
解答 解:cos33x+cos35x=(cos3x+cos5x)[cos23x+cos25x-cos3xcos5x]=2cosxcos4x[cos23x+cos25x-cos3xcos5x],
∵100°<x<200°,∴cosx≠0,400°<4x<800°,由于4x=450°或630°时,cos4x=0,
由cos33x+cos35x=8cos34xcos3x,
可知:x=$\frac{45{0}^{°}}{4}$,$\frac{63{0}^{°}}{4}$是此方程的两个根.
化为:cos23x+cos25x-cos3xcos5x=4cos24xcos2x,
∴$\frac{1+cos6x}{2}$+$\frac{1+cos10x}{2}$-cos3xcos5x=4×$\frac{1+cos8x}{2}$×$\frac{1+cos2x}{2}$,
化为:1+cos8xcos2x-cos3xcos5x=1+cos8xcos2x+cos5xcos3x,
可得cos5xcos3x=0,
∵100°<x<200°,∴300°<3x<600°,500°<5x<1000°,
由于3x=450°,5x=630°,810°,990°.
∴x=150°,或x=$\frac{63{0}^{°}}{5}$,$\frac{81{0}^{°}}{5}$,$\frac{99{0}^{°}}{5}$.
综上可得:所有根在角度制下度数数值之和=$\frac{450+630}{4}$+150+$\frac{630+810+990}{5}$=906.
故答案为:906.
点评 本题考查了“立方和公式”、倍角公式、和差化积,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
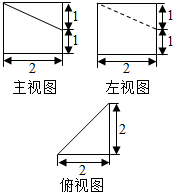
| A. | $\frac{23}{3}$ | B. | 4$\sqrt{2}$+$\sqrt{6}$+6 | C. | 6$\sqrt{2}$+6 | D. | 4$\sqrt{2}$+$\sqrt{6}$+8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com