
| ��ͣ��ʱ�� ��Сʱ�� | ��0��1] | ��1��2] | ��2��3] | ��3��4] |
| ��ͣ����a ��Ԫ�� |
���� ����������ɵñ���
����ͣ������aԪ������ͣ������bԪ������a��b=6��14��22��30���оٿɵ��ܵĻ����¼����ɸ��ʹ�ʽ�ɵã�
�����ɶ����¼��ĸ��ʹ�ʽ�ɵã�
��� �⣺����������ɵñ������£�
| ��ͣ��ʱ�� ��Сʱ�� | ��0��1] | ��1��2] | ��2��3] | ��3��4] |
| ��ͣ����a ��Ԫ�� | 6 | 14 | 22 | 30 |
���� ���⿼��ŵ���ͼ�����ʹ�ʽ���о��ǽ������Ĺؼ����������⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
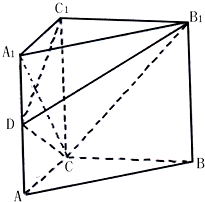 ij�Ҿ�װ����Ƶ���״����ͼ��ʾ��ֱ������ABC-A1B1C1�����У���ACB=90�㣬BCC1B1�DZ߳�Ϊ2����λ���ף��������Σ�AC=1����DΪ��AA1�ϵĶ��㣮
ij�Ҿ�װ����Ƶ���״����ͼ��ʾ��ֱ������ABC-A1B1C1�����У���ACB=90�㣬BCC1B1�DZ߳�Ϊ2����λ���ף��������Σ�AC=1����DΪ��AA1�ϵĶ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ؾ����㷨���������������Լ���ķ��� | |
| B�� | ����������������ʽ��ֵ�ķ��� | |
| C�� | ��Բ���Dz��������������ƽ�Բ������㷨����Բ���ʦ� | |
| D�� | ���Ͻ��۽Դ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-1���ȣ�0��1�� | B�� | ��-1��0���ȣ�1��+�ޣ� | C�� | ��-1��0���ȣ�0��1�� | D�� | ��-�ޣ�-1���ȣ�1��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{\sqrt{3}}{3}$ | D�� | $\frac{\sqrt{2}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3cm2 | B�� | 6cm2 | C�� | 9cm2 | D�� | 18cm2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com