
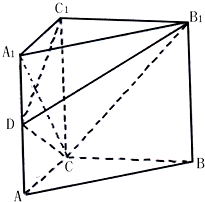
 某家居装饰设计的形状是如图所示的直三棱柱ABC-A1B1C1,其中,∠ACB=90°,BCC1B1是边长为2(单位:米)的正方形,AC=1,点D为棱AA1上的动点.
某家居装饰设计的形状是如图所示的直三棱柱ABC-A1B1C1,其中,∠ACB=90°,BCC1B1是边长为2(单位:米)的正方形,AC=1,点D为棱AA1上的动点.分析 (Ⅰ)证明AC⊥BC.AA1⊥BC.然后证明BC⊥平面ACC1A1.求出直三棱柱ABC-A1B1C1的表面积,即可求解需油漆费.
(Ⅱ)当点D为AA1的中点时,CD⊥平面B1C1D.当CD⊥C1D时,有CD⊥平面B1C1D,求出AD,推出结果即可.
解答 (本题满分12分)
解:(Ⅰ)因为BCC1B1是边长为2的正方形,所以BC=CC1=AA1=2.
因为∠ACB=90°,所以AC⊥BC.
又易知AA1⊥平面ABC,所以AA1⊥BC.
又AC∩AA1=A,所以BC⊥平面ACC1A1.
又AC=1,所以直三棱柱ABC-A1B1C1的表面积为${S_{ABC-{A_1}{B_1}{C_1}}}=\frac{1}{2}×2×1×2+2×2+1×2+\sqrt{{2^2}+{1^2}}×2=8+2\sqrt{5}$(平方米).
则需油漆费$({8+2\sqrt{5}})×40=320+80\sqrt{5}≈320+80×2.236≈499$(元).…(6分)
(Ⅱ)当点D为AA1的中点时,CD⊥平面B1C1D.证明如下:
由(Ⅰ)得BC⊥平面ACC1A1.
又BC∥B1C1,所以B1C1⊥平面ACC1A1.
所以B1C1⊥CD.
故当CD⊥C1D时,有CD⊥平面B1C1D,且此时有△C1A1D∽△DAC.
设AD=x,则$\frac{{{A_1}{C_1}}}{{{A_1}D}}=\frac{AD}{AC}$,即$\frac{1}{2-x}=\frac{x}{1}$,解得x=1.
此时$AD=1=\frac{1}{2}A{A_1}$,即当点D为AA1的中点时,CD⊥平面B1C1D.…(12分)
点评 本题考查直线与平面垂直判断的应用,几何体的表面积的求法,考查计算能力.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
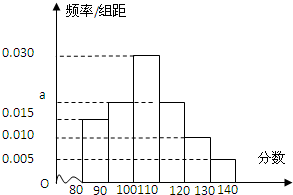 某校高一(1)班共有54人,如图是该班期中考试数学成绩的频率分布直方图,则成绩在[100,120]内的学生人数为( )
某校高一(1)班共有54人,如图是该班期中考试数学成绩的频率分布直方图,则成绩在[100,120]内的学生人数为( )| A. | 36 | B. | 27 | C. | 22 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{23}{3}$ | B. | $\frac{22}{3}$ | C. | $\frac{47}{6}$ | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{5}$ | B. | -1 | C. | $\frac{11}{5}$ | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{2}$ | C. | 5 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲停车时长 (小时) | (0,1] | (1,2] | (2,3] | (3,4] |
| 甲停车费a (元) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com