
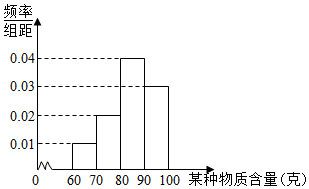
 ij��ҵ����������һ����Ʒ���м�⣬�ó�ÿ����Ʒ��ij�����ʺ�������λ���ˣ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
ij��ҵ����������һ����Ʒ���м�⣬�ó�ÿ����Ʒ��ij�����ʺ�������λ���ˣ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��| ��Ʒ���� | C | B | A |
| ijѺ���ʺ�����Χ | [60��70�� | [70��80�� | [80��100] |
���� ��������Ƶ�ʷֲ�ֱ��ͼ�ܹ��Ʋ�Ʒ�и����ʺ�����ƽ���������
�����ֲ�����ķ������������A��ƷΪ7����B��C��Ʒ��3������������εĿ���ȡֵΪ0��1��2��3���ֱ������Ӧ�ĸ��ʣ��ɴ�������εķֲ��к���ѧ������
��� �⣺����ƽ����$\overline{x}$=65��0.1+75��0.2+85��0.4+95��0.3=84��
����S2=��65-84��2��0.1+��75-84��2��0.2+��85-84��2��0.4+��95-84��2��0.3=89��
�����ֲ�����ķ�������A��Ʒ�г�ȡn1=10��0.7=7����
��B��Ʒ�г�ȡn2=10��0.2=2����
��C��Ʒ�г�ȡn3=10��0.1=1����
���������A��ƷΪ7����B��C��Ʒ��3����
��������εĿ���ȡֵΪ0��1��2��3��
P����=0��=$\frac{{C}_{3}^{0}{C}_{7}^{3}}{{C}_{10}^{3}}$=$\frac{7}{24}$��
P����=1��=$\frac{{C}_{3}^{1}{C}_{7}^{2}}{{C}_{10}^{3}}$=$\frac{21}{40}$��
P����=2��=$\frac{{C}_{3}^{2}{C}_{7}^{1}}{{C}_{10}^{3}}$=$\frac{7}{40}$��
P����=3��=$\frac{{C}_{3}^{3}{C}_{7}^{0}}{{C}_{10}^{3}}$=$\frac{1}{120}$��
��εķֲ���Ϊ��
| �� | 0 | 1 | 2 | 3 |
| P | $\frac{7}{24}$ | $\frac{21}{40}$ | $\frac{7}{40}$ | $\frac{1}{120}$ |
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��ͳ��������������ķֲ��С���ѧ�����Ȼ���֪ʶ����������������������ݴ���������Ӧ����ʶ���������������˼�롢��Ȼ���Ȼ˼��ȣ�


 ��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
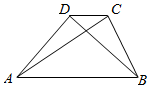
| A�� | $\overrightarrow{AB}$=3$\overrightarrow{CD}$ | B�� | $\overrightarrow{AC}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\overrightarrow{AD}$ | C�� | $\overrightarrow{BD}$=$\overrightarrow{AB}$-$\overrightarrow{AD}$ | D�� | $\overrightarrow{BC}$=-$\frac{2}{3}$$\overrightarrow{AB}$+$\overrightarrow{AD}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{\sqrt{3}}{3}$ | C�� | $\frac{\sqrt{2}}{2}$ | D�� | $\frac{\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
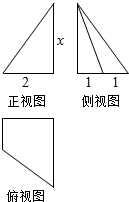
| A�� | 2 | B�� | $\frac{9}{2}$ | C�� | $\frac{3}{2}$ | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -5 | B�� | -1 | C�� | 0 | D�� | 1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com