
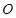 和点
和点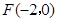 分别为双曲线
分别为双曲线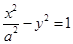 (
(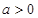 )的中心和左焦点,点
)的中心和左焦点,点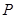 为双曲线右支上的任意一点,则
为双曲线右支上的任意一点,则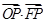 的取值范围为( )
的取值范围为( )A.[3- 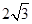 , , 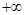 ) ) | B.[3+ 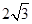 , , 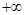 ) ) |
C.[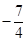 , , 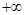 ) ) | D.[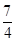 , , 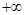 ) ) |
 设点P(x0,y0),则有
设点P(x0,y0),则有 (x0≥
(x0≥ ),解得y02=
),解得y02= (x0≥
(x0≥ ),
),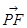 =(x0+2,y0),
=(x0+2,y0), =(x0,y0),所以
=(x0,y0),所以
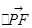 =x0(x0+2)+y02=x0(x0+2)+
=x0(x0+2)+y02=x0(x0+2)+ =
= +2x0-1,此二次函数对应的抛物线的对称轴为x0=-
+2x0-1,此二次函数对应的抛物线的对称轴为x0=- ,因为x0≥
,因为x0≥ ,
, 时,
时,
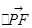 取得最小值
取得最小值
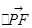 =
= ,故
,故
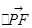
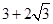 ,+∞),选B
,+∞),选B ,进而求得
,进而求得 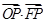 的表达式,利用二次函数的性质求得其最小值,则
的表达式,利用二次函数的性质求得其最小值,则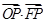 的取值范围可得.
的取值范围可得.

科目:高中数学 来源:不详 题型:单选题
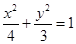 上有n个不同的点:P1 ,P2 ,…,Pn, 椭圆的右焦点为F,数列{|PnF|}是公差大于
上有n个不同的点:P1 ,P2 ,…,Pn, 椭圆的右焦点为F,数列{|PnF|}是公差大于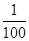 的等差数列, 则n的最大值是( )
的等差数列, 则n的最大值是( )| A.198 | B.199 | C.200 | D.201 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com