
分析 设P(4+$\sqrt{m}$cosθ,3+$\sqrt{m}$sinθ),由圆x2+y2-8x-6y+25-m=0上存在点P使$\overrightarrow{PA}•\overrightarrow{PB}=0$,得到$\overrightarrow{PA}•\overrightarrow{PB}$=24+m+10$\sqrt{m}$sin(θ+φ)=0,从而m-10$\sqrt{m}$+24=0,由此能求出m的最小值.
解答 解:∵圆x2+y2-8x-6y+25-m=0的圆心C(4,3),半径r=$\sqrt{m}$,
A(-1,0),B(1,0),
∴设P(4+$\sqrt{m}$cosθ,3+$\sqrt{m}$sinθ),
则$\overrightarrow{PA}$=(-5-$\sqrt{m}$cosθ,-3-$\sqrt{m}sinθ$),$\overrightarrow{PB}$=(-3-$\sqrt{m}$cosθ,-3-$\sqrt{m}sinθ$),
∵圆x2+y2-8x-6y+25-m=0上存在点P使$\overrightarrow{PA}•\overrightarrow{PB}=0$,
∴$\overrightarrow{PA}•\overrightarrow{PB}$=15+8$\sqrt{m}$cosθ+mcos2θ+9+6$\sqrt{m}$sinθ+msin2θ
=24+m+10$\sqrt{m}$sin(θ+φ)=0,
∴m-10$\sqrt{m}$+24=0,解得m=36或m=16.
∴m的最小值为16.
故答案为:16.
点评 本题考查实数值的最小值的求法,考查直线方程、圆的参数方程、向量的数量积等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


科目:高中数学 来源:2017届山西临汾一中高三10月月考数学(理)试卷(解析版) 题型:选择题
设点 和点
和点 分别是函数
分别是函数 和
和 图象上的点,且
图象上的点,且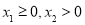 .若直线
.若直线 轴, 则
轴, 则 两点间的距离的最小值为( )
两点间的距离的最小值为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(文)试卷(解析版) 题型:解答题
某市组织500名志愿者参加敬老活动,为方便安排任务将所有志愿者按年龄(单位:岁)分组,得到的频率分布表如下.现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人担任联系人.
年龄(岁) | 频率 | |
第1组 |
| 0.1 |
第2组 |
| 0.1 |
第3组 |
| 0.4 |
第4组 |
| 0.3 |
第5组 |
| 0.1 |
(1)应分别在第1,2,3组中抽取志愿者多少人?
(2)从这6人中随机抽取2人担任本次活动的宣传员,求至少有1人年龄在第3组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是正方体的平面展开图,在这个正方体中,
如图是正方体的平面展开图,在这个正方体中,| A. | ③ | B. | ③④ | C. | ①③ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\sqrt{2}$,$\sqrt{2}$] | B. | [0,2$\sqrt{2}$] | C. | [-2$\sqrt{2}$,2$\sqrt{2}$] | D. | [-2,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com