
【题目】已知函数![]() 为定义域
为定义域![]() 上的奇函数,且在
上的奇函数,且在![]() 上是单调递增函数,函数
上是单调递增函数,函数![]() ,数列
,数列![]() 为等差数列,且公差不为0,若
为等差数列,且公差不为0,若![]() ,则
,则![]() ( )
( )
A.18B.9C.27D.81
【答案】C
【解析】
根据题意,由奇函数的性质可得f(﹣x)+f(x)=0,又由g(x)=f(x﹣3)+x且g(a1)+g(a2)+…+g(a9)=27,可得f(a1﹣3)+f(a2﹣3)+…+f(a9﹣3)+(a1+a2+…+a9)=27,结合等差数列的性质可得f(a1﹣5)=﹣f(a9﹣5)=f(5﹣a9),进而可得a1﹣5=5﹣a9,即a1+a9=10,进而计算可得答案.
根据题意,函数y=f(x)为定义域R上的奇函数,
则有f(﹣x)+f(x)=0,
∵g(x)=f(x﹣3)+x,
∴若g(a1)+g(a2)+…+g(a9)=27,
即f(a1﹣3)+a1+f(a2﹣3)+a2+…+f(a9﹣3)+a9=27,
即f(a1﹣3)+f(a2﹣3)+…+f(a9﹣3)+(a1+a2+…+a9)=27,
f(a1﹣3)+f(a2﹣3)+…+f(a9﹣3))+(a1﹣3+a2﹣3+…+a9﹣3)=0,
又由y=f(x)+x为定义域R上的奇函数,且在R上是单调函数,
且(a1﹣3)+(a9﹣3)=(a2﹣3)+(a8﹣3)=…=2(a5﹣3),
∴a5﹣3=0,
即a1+a9=a2+a8=…=2a5=6,
则a1+a2+…+a9=9a5=27;
故选:C.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 为椭圆上一动点,当
为椭圆上一动点,当![]() 的面积最大时,其内切圆半径为
的面积最大时,其内切圆半径为![]() ,设过点
,设过点![]() 的直线
的直线![]() 被椭圆
被椭圆![]() 截得线段
截得线段![]() ,
,
当![]() 轴时,
轴时,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若点![]() 为椭圆
为椭圆![]() 的左顶点,
的左顶点,![]() 是椭圆上异于左、右顶点的两点,设直线
是椭圆上异于左、右顶点的两点,设直线![]() 的斜率分别为
的斜率分别为![]() ,若
,若![]() ,试问直线
,试问直线![]() 是否过定点?若过定点,求该定点的坐标;若不过定点,请说明理由.
是否过定点?若过定点,求该定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 长轴的一个端点是抛物线
长轴的一个端点是抛物线![]() 的焦点,且椭圆焦点与抛物线焦点的距离是1。
的焦点,且椭圆焦点与抛物线焦点的距离是1。
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是椭圆
是椭圆![]() 的左右端点,
的左右端点,![]() 为原点,
为原点,![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的任意一点,直线
的任意一点,直线![]() 分别交
分别交![]() 轴于
轴于![]() ,问
,问![]() 是否为定值,说明理由。
是否为定值,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知美国苹果公司生产某款iphone手机的年固定成本为40万美元,每生产1万部还需要另外投入16美元,设苹果公司一年内共生产该款iphone手机![]() 万部并全部销售完,每万部的销售收入为
万部并全部销售完,每万部的销售收入为![]() 万元,且
万元,且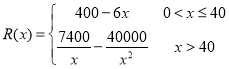 .
.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万部)的函数解析式;
(万部)的函数解析式;
(2)当年产量为多少万部时,苹果公司在该款手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com