
分析 (1)求出函数的导数,利用曲线f(x)在点(1,f(1))处的切线平行于x轴,求出a,然后判断函数的单调性,求解函数的最小值即可.
(2)令$g(x)=f(x)-f(\frac{1}{x})$,化简通过函数的导数,判断导函数的符号,然后通过x 的范围,判断两个数的大小.
(3)要证xexlnx+ex>x3,即证:$lnx+\frac{1}{x}>\frac{x^2}{e^x}$,令$h(x)=\frac{x^2}{e^x}$,利用函数的导数,判断函数的单调性求出函数的最小值,即可证明结果.
解答 (本小题满分12分)
解:(1)f'(x)=$\frac{a}{x}-\frac{1}{x^2}(x>0)$,根据题意知f'(1)=0,即a=1,∴$f(x)=lnx+\frac{1}{x}$,
…(2分)
∴f'(x)=$\frac{1}{x}-\frac{1}{x^2}=\frac{x-1}{x^2}$,∴当0<x<1时,f'(x)<0,f(x)单调递减;
当x>1时,f'(x)>0,f(x)单调递增;
∴f(x)min=f(1)=1. …(4分)
(2)令$g(x)=f(x)-f(\frac{1}{x})$=$lnx+\frac{1}{x}-[ln(\frac{1}{x})+x]$=$2lnx+\frac{1}{x}-x$,
$g'(x)=\frac{2}{x}-\frac{1}{x^2}-1=-\frac{{{{(x-1)}^2}}}{x^2}≤0$,
∴g(x)在(0,+∞)上单调递减…(6分)
又∵g(1)=0∴当0<x<1时,g(x)>g(1)=0,$f(x)>f(\frac{1}{x})$;
当x>1时,g(x)<g(1)=0,$f(x)<f(\frac{1}{x})$;
当x=1时,g(x)=0,$f(x)=f(\frac{1}{x})$.…(8分)
(3)要证xexlnx+ex>x3,即证:$lnx+\frac{1}{x}>\frac{x^2}{e^x}$…(10分)
令$h(x)=\frac{x^2}{e^x}$,即证∴f(x)>h(x),$h'(x)=\frac{{2x{e^x}-{e^x}{x^2}}}{{{e^{2x}}}}$=$\frac{{2x-{x^2}}}{e^x}$,
∴当0<x<2时,h'(x)>0,h(x)单调递增;
当x>2时,h'(x)<0,h(x)单调递减;∴h(x)max=h(2)=$\frac{4}{e^2}<1$,
又由(1)知f(x)min=1,∴f(x)≥1,∴f(x)>h(x),得证.…(12分)
附加题:(每小题(5分),共15分)
点评 本题考查函数的导数的综合应用,函数的单调性以及函数的最值的求法,考查转化思想以及计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
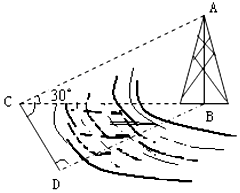 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与∠BCD=75°,∠BDC=60°,CD=20mD.现测得,并在点C测得塔顶A的仰角为30°,求塔高AB.
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与∠BCD=75°,∠BDC=60°,CD=20mD.现测得,并在点C测得塔顶A的仰角为30°,求塔高AB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
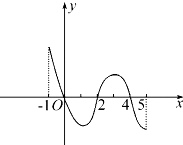 已知函数f(x)的定义域为[-1,5],部分对应值如表:
已知函数f(x)的定义域为[-1,5],部分对应值如表:| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 2 | 0 | 2 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com