
分析 (1)由f(0)=1,可得m=2,求出f(x)的导数,求得切线的斜率,由点斜式方程可得切线的方程;
(2)由零点的概念,化简函数y,令x2-x1=t(t>0),$g(t)=\frac{{{e^t}-1}}{{{e^t}+1}}-t(t>0)$,求出导数,求得单调性,即可得到所求值域;
(3)由f(x)>0得mex-x-1>0,即有$m>\frac{x+1}{e^x}$,令$u(x)=\frac{x+1}{e^x}$,求出导数,单调区间和最大值;又令h(m)=(e-1)lnm-m+1,求出导数,求得单调区间,即可得到所求大小关系.
解答 解:(1)当x=0时,f(0)=m-1=1⇒m=2,
f′(x)=2ex-1,f′(0)=2-1=1,
∴所求切线方程y=x+1,即x-y+1=0;
(2)由题意,$m{e^{x_1}}-{x_1}-1=0$,$m{e^{x_2}}-{x_2}-1=0$.
相减可得m(e${\;}^{{x}_{2}}$-e${\;}^{{x}_{1}}$)=x2-x1,
即有$y=\frac{{{e^{x_2}}-{e^{x_1}}}}{{{e^{x_2}}+{e^{x_1}}}}-m({e^{x_2}}-{e^{x_1}})$=$\frac{{{e^{x_2}}-{e^{x_1}}}}{{{e^{x_2}}+{e^{x_1}}}}-({x_2}-{x_1})$
=$\frac{{{e^{{x_2}-{x_1}}}-1}}{{{e^{{x_2}-{x_1}}}+1}}-({x_2}-{x_1})$,
令x2-x1=t(t>0),$g(t)=\frac{{{e^t}-1}}{{{e^t}+1}}-t(t>0)$,
又${g^/}(t)=\frac{{-{e^{2t}}-1}}{{{{({e^t}+1)}^2}}}<0$,
∴g(t)在(0,+∞)上单调递减,
∴g(t)<g(0)=0,
∴g(t)∈(-∞,0),
∴$y=({e^{x_2}}-{e^{x_1}})(\frac{1}{{{e^{x_2}}+{e^{x_1}}}}-m)$的值域为(-∞,0);
(3)由f(x)>0得mex-x-1>0,即有$m>\frac{x+1}{e^x}$,
令$u(x)=\frac{x+1}{e^x}$,则${u^/}(x)=\frac{-x}{e^x}$,
令u′(x)>0⇒x<0,u′(x)<0⇒x>0,
∴u(x)在(-∞,0)上单调递增,在(0,+∞)上单调递减.
∴u(x)max=u(0)=1,∴m>1.
又令h(m)=(e-1)lnm-m+1,
则${h^/}(m)=\frac{e-1}{m}-1=\frac{e-1-m}{m}$.
令h′(m)>0⇒m<e-1,h′(m)<0⇒m>e-1,又m>1
∴h(m)在(1,e-1)上单调递增,在(e-1,+∞)上单调递减
又h(1)=-1+1=0,h(e)=e-1-e+1=0
∴当1<m<e时,h(m)>0⇒(e-1)lnm-m+1>0,
即(e-1)lnm>m-1
∴em-1<me-1,
同理,当m=e时,em-1=me-1,当m>e时,em-1>me-1.
综上,当1<m<e时,em-1<me-1
当m=e时,em-1=me-1,
当m>e时,em-1>me-1.
点评 本题考查导数的运用:求切线的方程和单调区间,考查函数方程的转化思想,以及单调性的运用,考查化简整理的运算能力,属于中档题.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
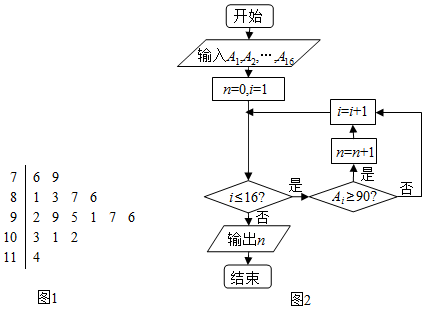
| A. | 6 | B. | 10 | C. | 7 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
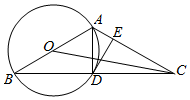 如图,以△ABC的边AB为直径作⊙O,⊙O与边BC的交点D恰为BC边的中点,过点D作DE⊥AC于点E.
如图,以△ABC的边AB为直径作⊙O,⊙O与边BC的交点D恰为BC边的中点,过点D作DE⊥AC于点E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com