
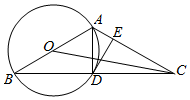
 如图,以△ABC的边AB为直径作⊙O,⊙O与边BC的交点D恰为BC边的中点,过点D作DE⊥AC于点E.
如图,以△ABC的边AB为直径作⊙O,⊙O与边BC的交点D恰为BC边的中点,过点D作DE⊥AC于点E.分析 (Ⅰ)连接OD.证明OD∥AC.推出DE⊥OD,得到DE是⊙O的切线.
(Ⅱ)说明AD⊥BC.求出∠ADE=30°.在直角三角形AED与在直角三角形DEC中求解所求比值即可.
解答 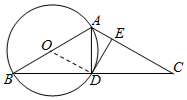 解:(Ⅰ)如图,连接OD.
解:(Ⅰ)如图,连接OD.
因为O是AB的中点,D是BC的中点,
所以 OD∥AC.
因为DE⊥AC,所以DE⊥OD,
所以DE是⊙O的切线.…(5分)
(Ⅱ)因为AB是⊙O的直径,点D在⊙O上,所以AD⊥BC.
又D是BC的中点,所以 AB=AC.故∠ACD=∠B=30°.
因为DE⊥AC,所以∠ADE=30°.在直角三角形AED中,$\frac{AE}{DE}=tan{30°}$;
在直角三角形DEC中,$\frac{DE}{DC}=sin{30°}$.
于是$\frac{AE}{DE}=\frac{1}{2}×\frac{{\sqrt{3}}}{3}=\frac{{\sqrt{3}}}{6}$.…(10分)
点评 本题考查直线与圆的位置关系的应用,三角形的解法,考查计算能力.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥1} | B. | $\left\{{x\left|{x≥\frac{1}{2}}\right.}\right\}$ | C. | {x|0<x≤1} | D. | $\left\{{x\left|{0<x≤\frac{1}{2}}\right.}\right\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于直线x=$\frac{13π}{12}$对称 | B. | 关于点(-$\frac{π}{12}$,0)对称 | ||
| C. | 关于直线x=-$\frac{7π}{12}$对称 | D. | 关于点($\frac{π}{4}$,0)对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0),|φ|<$\frac{π}{2}$的部分图象如图所示,则f($\frac{π}{4}$)等于( )
函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0),|φ|<$\frac{π}{2}$的部分图象如图所示,则f($\frac{π}{4}$)等于( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com