Question

6．△ABC中，$|{\overrightarrow{AB}}|=\sqrt{3}$，$|{\overrightarrow{AC}}|=1$，D是BC边中垂线上任意一点，则$\overrightarrow{AD}•\overrightarrow{CB}$的值是（　　）

• A． 1
• B． $\sqrt{2}$
• C． $\sqrt{3}$
• D． -1

Answer 1

分析 由题意作图辅助，设BC的中点为E，从而可得$\overrightarrow{AD}•\overrightarrow{CB}$=（$\overrightarrow{AE}$-$\overrightarrow{DE}$）•$\overrightarrow{CB}$=$\overrightarrow{AE}$•$\overrightarrow{CB}$=$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$）•（$\overrightarrow{AB}$-$\overrightarrow{AC}$），从而解得．

解答 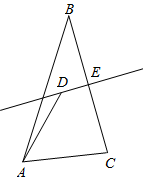解：由题意作图如右图，
设BC的中点为E，
则$\overrightarrow{AD}•\overrightarrow{CB}$=（$\overrightarrow{AE}$-$\overrightarrow{DE}$）•$\overrightarrow{CB}$
=$\overrightarrow{AE}$•$\overrightarrow{CB}$-$\overrightarrow{DE}$•$\overrightarrow{CB}$
=$\overrightarrow{AE}$•$\overrightarrow{CB}$
=$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$）•（$\overrightarrow{AB}$-$\overrightarrow{AC}$）
=$\frac{1}{2}$（${\overrightarrow{AB}}^{2}$-${\overrightarrow{AC}}^{2}$）=1，
故选：A．

点评 本题考查了数形结合的思想应用及平面向量的线性运算与数量积的应用．