
分析 通过定义可知数列数列{pn}、数列{qn}均为周期数列,进而可知数列{pn•qn}中每12项的和循环一次,进而计算可得结论.
解答 解:由题意可知,p1=1,p2=2,p3=4,p4=8,p5=1,p6=2,p7=4,p8=8,p9=1,p10=2,p11=4,p12=8,p13=1,…,
又pn是4阶等和数列,因此该数列将会照此规律循环下去,
同理,q1=-1,q2=-1,q3=1,q4=-1,q5=-1,q6=1,q7=-1,q8=-1,q9=1,q10=-1,q11=-1,q12=1,q13=-1,…,
又qn是3阶等积数列,因此该数列将会照此规律循环下去,
由此可知对于数列{pn•qn},每12项的和循环一次,
易求出p1•q1+p2•q2+…+p12•q12=-15,
因此S2016中有168组循环结构,
故S2016=-15×168=-2520,
故答案为:-2520.
点评 本题主要考查非常规数列求和问题,对学生的逻辑思维能力提出很高要求,属于一道难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在如图所示的直三棱柱ABC-A1B1C1,AC=1,BC=$\sqrt{2}$,AB=$\sqrt{3}$,侧棱AA1=1,点D,M分别为A1B,B1C1的中点.
在如图所示的直三棱柱ABC-A1B1C1,AC=1,BC=$\sqrt{2}$,AB=$\sqrt{3}$,侧棱AA1=1,点D,M分别为A1B,B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
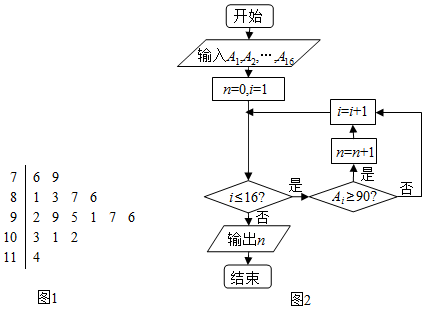
| A. | 6 | B. | 10 | C. | 7 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com