练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．函数y=sinx-2x的导数是（　　）
    A．cosx-2xB．cosx-2x•ln2C．-cosx+2xD．-cosx-2x•ln2

    分析 利用导数的运算法则即可得出．

    解答 解：∵y=sinx-2x，
    ∴y′=cosx-2x•ln2
    故选：B．

    点评 本题考查了导数的运算法则，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=|2x-a|+|2x+3|，g（x）=|x-1|+2．
    （1）解不等式g（x）＜|x-2|+2；
    （2）若对任意x1∈R都有x2∈R，使得f（x1）=g（x2）成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知α为第二象限角，则$\frac{α}{2}$所在的象限是（　　）
    A．第一或第二象限B．第二或第三象限C．第一或第三象限D．第二或第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．函数f（x）=x3-ax-1．
    （1）当a=8时，求函数f（x）在x=0处的切线方程．
    （2）讨论f（x）=x3-ax-1的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．在平面直角坐标系xOy中，已知圆O：x2+y2=4和点P（-1，0），过点P的直线l交圆O于A、B两点
    （1）若|AB|=2$\sqrt{3}$，求直线l的方程；
    （2）设弦AB的中点为M，求点M的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的左、右焦点和短轴的一个端点构成边长为4的正三角形．
    （1）求椭圆C的方程；
    （2）过右焦点F2的直线l与椭圆C相交于A、B两点，若$\overrightarrow{A{F}_{2}}$=2$\overrightarrow{{F}_{2}B}$，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知数列{an}满足a1=2，点（an，an+1）在直线y=3x+2上，数列{bn}满足b1=2，$\frac{{b}_{n+1}}{{a}_{n+1}}$=$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$
    （1）求b2的值；
    （2）求证数列{an+1}为等比数列，并求出数列{an}的通项公式；
    （3）求证：2-$\frac{1}{2•{3}^{n-1}}$≤（1+$\frac{1}{{b}_{1}}$）（1+$\frac{1}{{b}_{2}}$）…（1+$\frac{1}{{b}_{n}}$）＜$\frac{33}{16}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．用与球心距离为1的平面去截球所得的截面面积为π，则球的表面积为（　　）
    A．2πB．4πC．8πD．$\frac{8}{3}π$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

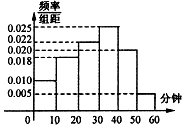    18．北京时间3月15日下午，谷歌围棋人工智能AlphaGo与韩国棋手李世石进行最后一轮较量，AlphaGo获得本场比赛胜利，最终人机大战总比分定格在1：4．人机大战也引发全民对围棋的关注，某学校社团为调查学生学习围棋的情况，随机抽取了100名学生进行调查．根据调查结果绘制的学生日均学习围棋时间的频率分布直方图（如图所示），将日均学习围棋时间不低于40分钟的学生称为“围棋迷”．
    非围棋迷围棋迷合计
    男301545
    女451055
    合计7525100
    （1）根据已知条件完成如图列联表，并据此资料判断你是否有95%的把握认为“围棋迷”与性别有关？
    （2）将上述调查所得到的频率视为概率．现在从该地区大量学生中，采用随机抽样方法每次抽取1名学生，抽取3次，记所抽取的3名学生中的“围棋迷”人数为X．若每次抽取的结果是相互独立的，求X的分布列，期望E（X）和方差D（X）．
    附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
    P（x2≥k0）0.050.010
    k03.746.63

    查看答案和解析>>

    同步练习册答案