练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．（x2-4）（x+$\frac{1}{x}$）9的展开式中x3的系数为-210．（用数字填写答案）

    分析 把（x+$\frac{1}{x}$）9按照二项式定理展开，可得（x2-4）（x+$\frac{1}{x}$）9的展开式中x3的系数．

    解答 解：∵（x2-4）（x+$\frac{1}{x}$）9=（x2-4）（${C}_{9}^{0}$•x9+${C}_{9}^{1}$•x7+${C}_{9}^{2}$•x5+…+${C}_{9}^{8}$•x-7+${C}_{9}^{9}$•x-9），
    故它的展开式中x3的系数为${C}_{9}^{4}$+（-4）•${C}_{9}^{3}$=126-336=-210，
    故答案为：-210．

    点评 本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    7．已知边长为2的正三角形ABC，P，M满足|AP|=1，$\overrightarrow{PM}$=$\overrightarrow{MC}$，则$\overrightarrow{BM}$2的最小值是（　　）
    A．$\frac{9-2\sqrt{3}}{4}$B．$\frac{11-3\sqrt{3}}{4}$C．$\frac{13-4\sqrt{3}}{4}$D．$\frac{15-5\sqrt{3}}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．设函数f（x）=x（lnx-ax）（a∈R）在区间（0，2）上有两个极值点，则a的取值范围是（　　）
    A．$（-\frac{1}{2}，0）$B．$（0，\frac{ln2+1}{4}）$C．$（\frac{1}{2}，1）$D．$（\frac{ln2+1}{4}，\frac{1}{2}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．对于函数y=f（x），若存在区间[a，b]，当x∈[a，b]时的值域为[ka，kb]（k＞0），则称y=f（x）为k倍值函数．若f（x）=lnx+x是k倍值函数，则实数k的取值范围是（　　）
    A．$（{0，1+\frac{1}{e}}）$B．$（{1，1+\frac{1}{e}}）$C．（1，1+e）D．（1，1+e2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

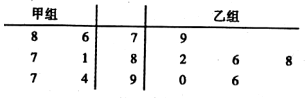    12．以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩（单位：分），规定85分以上（含85分）为优秀，现分别从甲、乙两组中随机选取一名同学的数学成绩，则两人成绩都为优秀的概率是（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{2}{3}$D．$\frac{1}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=2lnx+x2-2ax（a＞0）．
    （I）讨论函数f（x）的单调性；
    （Ⅱ）若函数f（x）有两个极值点x1，x2（x1＜x2），且f（x1）-f（x2）≥$\frac{3}{2}$-2ln2恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．函数f（x）=x2•cosx在$[{-\frac{π}{2}，\frac{π}{2}}]$的图象大致是（　　）
    A．B．
    C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知a，b，c分别是△ABC的内角A，B，C的对边，2sin$\frac{7π}{6}$sin（$\frac{π}{6}$+C）+cosC=-$\frac{1}{2}$．
    （1）求C；
    （2）若c=$\sqrt{13}$，且△ABC面积为3$\sqrt{3}$，求sinA+sinB的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）离心率为$\frac{1}{2}$，过椭圆上一点P分别作斜率为$\frac{b}{a}，-\frac{b}{a}$的两条直线，这两条直线与x轴分别交于点M，N两点，且|OM|2+|ON|2=8．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）设直线PM，PN与椭圆C的另外两个交点分别为Q，R，当点P的横坐标为1时，求△PQR的面积．

    查看答案和解析>>

    同步练习册答案