
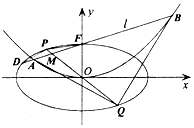
 ��ƽ��ֱ������ϵxOy�У�������E��x2=4y�Ľ���F����Բ$C��\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$��a��b��0����һ�����㣮����F��б��Ϊk��k��0����ֱ��l����ԲC����һ��D����������E��A��B���㣬�߶�DF���е�ΪM��ֱ��OM����ԲC��P��Q���㣬��ֱ��OM��б��Ϊk'������$k•k'=-\frac{1}{4}$��
��ƽ��ֱ������ϵxOy�У�������E��x2=4y�Ľ���F����Բ$C��\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$��a��b��0����һ�����㣮����F��б��Ϊk��k��0����ֱ��l����ԲC����һ��D����������E��A��B���㣬�߶�DF���е�ΪM��ֱ��OM����ԲC��P��Q���㣬��ֱ��OM��б��Ϊk'������$k•k'=-\frac{1}{4}$������ ��1�����������ֱ��l�ķ���Ϊy=kx+1������Բ�������������D�����꣬�����е����깫ʽ���M�����꣬�õ�OM��б�ʽ����֪���aֵ������Բ���̿���
��2���ɣ�1����֪��D������Ϊ��$-\frac{8k}{1+4{k}^{2}}��\frac{1-4{k}^{2}}{1+4{k}^{2}}$������F��0��1�����ɵ�|DF|����$\left\{\begin{array}{l}{{x}^{2}=4y}\\{y=kx+1}\end{array}\right.$�������ҳ���ʽ���|AB|�����ֱ��OM�ķ���Ϊy=-$\frac{1}{4k}x$����$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{y=-\frac{1}{4k}x}\end{array}\right.$�����P��Q�����꣬�ɵ㵽ֱ�ߵľ��빫ʽ��õ�P��ֱ��kx-y+1=0�ľ���${d}_{1}=\frac{||k|•\sqrt{1+4{k}^{2}}+k|}{|k|•\sqrt{1+{k}^{2}}}$����Q��ֱ��kx-y+1=0�ľ�${d}_{2}=\frac{||k|•\sqrt{1+4{k}^{2}}-k|}{|k|•\sqrt{1+{k}^{2}}}$�����������������ʽ�����������û�������ʽ���ʵ���˵����ֵ��ȡ�����ֵʱֱ��l�ķ��̣�
��� �⣺��1�����������ֱ��l�ķ���Ϊy=kx+1��
����$\left\{\begin{array}{l}{y=kx+1}\\{\frac{{x}^{2}}{{a}^{2}}+{y}^{2}=1}\end{array}\right.$���ã�1+a2k2��x2+2a2kx=0��
��ã�${x}_{D}=-\frac{2{a}^{2}k}{1+{a}^{2}{k}^{2}}$��${y}_{D}=\frac{1-{a}^{2}{k}^{2}}{1+{a}^{2}{k}^{2}}$��
��M��$-\frac{{a}^{2}k}{1+{a}^{2}{k}^{2}}$��$\frac{1}{1+{a}^{2}{k}^{2}}$������k��=${k}_{OM}=-\frac{1}{{a}^{2}k}$��
��$k•k'=-\frac{1}{4}$����$k��•k=-\frac{1}{{a}^{2}}=-\frac{1}{4}$��
��a2=4��
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{4}+{y}^{2}=1$��
��2���ɣ�1����֪��D������Ϊ��$-\frac{8k}{1+4{k}^{2}}��\frac{1-4{k}^{2}}{1+4{k}^{2}}$������F��0��1����
��|DF|=$\sqrt{��-\frac{8k}{1+4{k}^{2}}��^{2}+��\frac{1-4{k}^{2}}{1+4{k}^{2}}-1��^{2}}=\frac{8|k|\sqrt{1+{k}^{2}}}{1+4{k}^{2}}$��
��$\left\{\begin{array}{l}{{x}^{2}=4y}\\{y=kx+1}\end{array}\right.$����x2-4kx-4=0��
��=16k2+16��0�������
��A��x1��y1����B��x2��y2������x1+x2=4k��x1x2=-4��
���$|AB|=\sqrt{��1+{k}^{2}��[��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{��1+{k}^{2}����16{k}^{2}+16��}=4��{k}^{2}+1��$��
�����⣬ֱ��OM�ķ���Ϊy=-$\frac{1}{4k}x$��
��$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{y=-\frac{1}{4k}x}\end{array}\right.$���ã�1+4k2��x2-16k2=0��
��Ȼ����=-4��1+4k2����-16k2����0���������x=$��\frac{4|k|}{\sqrt{1+4{k}^{2}}}$��
������${x}_{P}=\frac{4|k|}{\sqrt{1+4{k}^{2}}}$����${y}_{P}=-\frac{1}{4k}{x}_{P}=��-\frac{1}{4k}��•\frac{4|k|}{\sqrt{1+4{k}^{2}}}=-\frac{|k|}{k•\sqrt{1+4{k}^{2}}}$��
���P������Ϊ��$\frac{4|k|}{\sqrt{1+4{k}^{2}}}��-\frac{|k|}{k•\sqrt{1+4{k}^{2}}}$��������Q������Ϊ��$-\frac{4|k|}{\sqrt{1+4{k}^{2}}}��\frac{|k|}{k•\sqrt{1+4{k}^{2}}}$����
��P��ֱ��kx-y+1=0�ľ���${d}_{1}=\frac{||k|•\sqrt{1+4{k}^{2}}+k|}{|k|•\sqrt{1+{k}^{2}}}$��
��Q��ֱ��kx-y+1=0�ľ���${d}_{2}=\frac{||k|•\sqrt{1+4{k}^{2}}-k|}{|k|•\sqrt{1+{k}^{2}}}$��
��${S}_{1}=\frac{1}{2}•|DF|•{d}_{1}=\frac{1}{2}•\frac{8|k|\sqrt{1+{k}^{2}}}{1+4{k}^{2}}•\frac{||k|•\sqrt{1+4{k}^{2}}+k|}{|k|•\sqrt{1+{k}^{2}}}$=$\frac{4||k|•\sqrt{1+4{k}^{2}}+k|}{1+4{k}^{2}}$��
${S}_{2}=\frac{1}{2}•|AB|•{d}_{2}$=$\frac{1}{2}•4��{k}^{2}+1��•\frac{||k|•\sqrt{1+4{k}^{2}}-k|}{|k|•\sqrt{1+{k}^{2}}}$=$\frac{2\sqrt{{k}^{2}+1}•||k|•\sqrt{1+4{k}^{2}}-k|}{|k|}$��
��S1S2=$\frac{8\sqrt{{k}^{2}+1}|{k}^{2}��1+4{k}^{2}��-{k}^{2}|}{��1+4{k}^{2}��|k|}=\frac{32{k}^{4}\sqrt{{k}^{2}+1}}{��1+4{k}^{2}��|k|}$=$\frac{32{k}^{2}|k|\sqrt{{k}^{2}+1}}{1+4{k}^{2}}$��
��${S_1}•{S_2}=��{k^2}$��
��$��=\frac{32|k|\sqrt{{k}^{2}+1}}{1+4{k}^{2}}$=$\frac{16}{\sqrt{3}}•\frac{2\sqrt{3{k}^{2}}•\sqrt{{k}^{2}+1}}{1+4{k}^{2}}��\frac{16}{\sqrt{3}}•\frac{3{k}^{2}+��{k}^{2}+1��}{1+4{k}^{2}}$=$\frac{16\sqrt{3}}{3}$��
���ҽ���3k2=k2+1����k=$��\frac{\sqrt{2}}{2}$ʱ���Ⱥų�����
��ʵ���˵����ֵΪ$\frac{16\sqrt{3}}{3}$����ȡ���ֵʱ��ֱ�߷���Ϊ$y=��\frac{\sqrt{2}}{2}x+1$��
���� ���⿼����Բ�ļ����ʣ�������ֱ������Բ��������λ�ù�ϵ��Ӧ�ã�����������������������������ѹ���⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���m��n�����Φ£���ôm������ɵĽǺ�n������ɵĽ���� | |
| B�� | ���m��n��m�ͦ���n�Φ£���ô���ͦ� | |
| C�� | ������Φ£�m?������ôm�Φ� | |
| D�� | ���m�ͦ���n�Φ�����ôm��n |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | s1��s2��s3 | B�� | s1��s3��s2 | C�� | s3��s2��s1 | D�� | s3��s1��s2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ʯ�Ӱڳ���ͼ��ʾ��������״��������5��9��14��20����Ϊ����������������ͼ�εĹ��ɣ������еĵ�100���a100=5252��
��ʯ�Ӱڳ���ͼ��ʾ��������״��������5��9��14��20����Ϊ����������������ͼ�εĹ��ɣ������еĵ�100���a100=5252���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ����ʹ��ѧ�� | ������ʹ��ѧ�� | �ܼ� | |
| ѧϰ�ɼ����� | 40 | ||
| ѧϰ�ɼ�һ�� | 30 | ||
| �ܼ� | 100 |
| P��K2��k0�� | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{6}}}{4}$ | B�� | $\frac{{\sqrt{10}}}{4}$ | C�� | $\frac{{\sqrt{15}}}{5}$ | D�� | $\frac{9}{10}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com