
| 善于使用学案 | 不善于使用学案 | 总计 | |
| 学习成绩优秀 | 40 | ||
| 学习成绩一般 | 30 | ||
| 总计 | 100 |
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
分析 (1)由随机抽查这100名学生中的一名学生,抽到善于使用学案的学生的概率是0.6,可得表格;
(2)计算K2,与临界值比较,可得结论;
(3)由(2)问结果可知,应该采用分层抽样的方法较为合理.
解答 解:(1)
| 善于使用学案 | 不善于使用学案 | 总计 | |
| 学习成绩优秀 | 40 | 10 | 50 |
| 学习成绩一般 | 20 | 30 | 50 |
| 总计 | 60 | 40 | 100 |
点评 本题考查独立性检验知识,考查分层抽样,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | 1008 | C. | 504 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
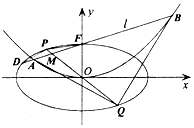 在平面直角坐标系xOy中,抛物线E:x2=4y的焦点F是椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一个顶点.过点F且斜率为k(k≠0)的直线l交椭圆C于另一点D,交抛物线E于A、B两点,线段DF的中点为M,直线OM交椭圆C于P、Q两点,记直线OM的斜率为k',满足$k•k'=-\frac{1}{4}$.
在平面直角坐标系xOy中,抛物线E:x2=4y的焦点F是椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一个顶点.过点F且斜率为k(k≠0)的直线l交椭圆C于另一点D,交抛物线E于A、B两点,线段DF的中点为M,直线OM交椭圆C于P、Q两点,记直线OM的斜率为k',满足$k•k'=-\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
| 18岁至31岁 | 8 | 12 | 20 | 60 | 140 | 150 |
| 32岁至44岁 | 12 | 28 | 20 | 140 | 60 | 150 |
| 45岁至59岁 | 25 | 50 | 80 | 100 | 225 | 450 |
| 60岁及以上 | 25 | 10 | 10 | 18 | 5 | 2 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
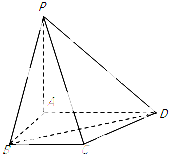 如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2.求二面角A-PD-C的余弦值.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2.求二面角A-PD-C的余弦值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$cm/s | B. | $\frac{1}{3}$cm/s | C. | $\frac{1}{4}$cm/s | D. | $\frac{1}{5}$cm/s |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com