
分析 (1)使用二倍角公式求出sin(2α+$\frac{π}{4}$),判断出2α+$\frac{π}{4}$的范围,使用同角三角函数的关系求出cos(2α+$\frac{π}{4}$);
(2)使用和角的余弦公式计算.
解答 解:(1)sin(2α+$\frac{π}{4}$)=2sin(α+$\frac{π}{8}$)cos(α+$\frac{π}{8}$)=$\frac{\sqrt{3}}{2}$.
∵α∈($\frac{π}{8}$,$\frac{π}{4}$),∴2α+$\frac{π}{4}$∈($\frac{π}{2}$,$\frac{3π}{4}$),∴cos(2α+$\frac{π}{4}$)=-$\sqrt{1-si{n}^{2}(2α+\frac{π}{4})}$=-$\sqrt{1-\frac{3}{4}}$=-$\frac{1}{2}$.
(2)∵β∈($\frac{π}{4}$,$\frac{π}{2}$),∴2β-$\frac{π}{4}$∈($\frac{π}{4}$,$\frac{3π}{4}$),∴sin(2β-$\frac{π}{4}$)=$\sqrt{1-co{s}^{2}(2β-\frac{π}{4})}$=$\frac{4}{5}$.
∴cos(2α+2β)=cos[(2α+$\frac{π}{4}$)+(2β-$\frac{π}{4}$)]=cos(2α+$\frac{π}{4}$)cos(2β-$\frac{π}{4}$)-sin(2α+$\frac{π}{4}$)sin(2β-$\frac{π}{4}$)
=-$\frac{1}{2}$×$\frac{3}{5}$-$\frac{\sqrt{3}}{2}$×$\frac{4}{5}$=$\frac{-3-4\sqrt{3}}{10}$.
点评 本题考查了三角函数的恒等变换,两角和的余弦公式,观察角的特点是解题关键.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | a=0,b=-3 | B. | a=-3,b=0 | C. | a=3,b=0 | D. | a=0,b=3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>1或-1<x<0} | B. | {x|x>1或x<-1} | C. | {x|0<x<1或x<-1} | D. | {x|-1<x<1且x≠0} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
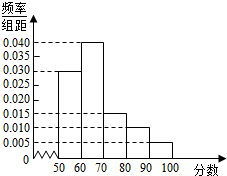 根据某组调查数据制作的频率分布直方图如图所示,则该组数据中的数位于区间(60,70)内的频率是( )
根据某组调查数据制作的频率分布直方图如图所示,则该组数据中的数位于区间(60,70)内的频率是( )| A. | 0.004 | B. | 0.04 | C. | 0.4 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ab有最大值$\frac{1}{4}$ | B. | $\frac{1}{a}$+$\frac{1}{b}$有最小值5 | ||
| C. | $\sqrt{a}$+$\sqrt{2b}$有最大值1+$\sqrt{2}$ | D. | a2+4b2有最小值$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com