
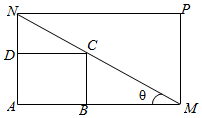
 ��ͼ��ʾ����һ���λ�̳ABCD������һ������ľ��λ�̳AMPN��Ҫ��M��AB���ӳ����ϣ�N��AD���ӳ����ϣ��ҶԽ���MN����C����֪AB=3�ף�AD=2�ף��Ǿ���AMPN�����ΪSƽ���ף�
��ͼ��ʾ����һ���λ�̳ABCD������һ������ľ��λ�̳AMPN��Ҫ��M��AB���ӳ����ϣ�N��AD���ӳ����ϣ��ҶԽ���MN����C����֪AB=3�ף�AD=2�ף��Ǿ���AMPN�����ΪSƽ���ף����� ��1�����AN��AM�����ɽ���������ϵ��
��i����AN=x�ף������AM�ij������ɱ�ʾ������AMPN�������
��ii���ɡ�BMC=�ȣ�rad�����������α�ʾ��AM��AN�ij��ȣ����ɱ�ʾ��S���ڦȵĺ�������ʽ��
��2��ѡ��ii���еĺ�����ϵʽ�������ɻ�������ʽ���������ֵ��
��� 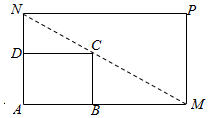 �⣺��1����i����Rt��CDN��Rt��MBC����$\frac{DN}{BC}$=$\frac{DC}{BM}$��
�⣺��1����i����Rt��CDN��Rt��MBC����$\frac{DN}{BC}$=$\frac{DC}{BM}$��
��$\frac{x-2}{2}=\frac{3}{BM}$����BM=$\frac{6}{x-2}$��
����$\frac{DN}{AN}=\frac{DC}{AM}$����AM=$\frac{3x}{x-2}$
��S=AN•AM=$\frac{3{x}^{2}}{x-2}$����x��2��
��ii����Rt��MBC��tan��=$\frac{BC}{MB}=\frac{2}{MB}$����MB=$\frac{2}{tan��}$����AM=3+$\frac{2}{tan��}$��
��Rt��CDN�У�tan��=$\frac{DN}{DC}=\frac{DN}{3}$����DN=3tan�ȣ���AN=2+3tan�ȣ�
��S=AM•AN=��3+$\frac{2}{tan��}$��•��2+3tan�ȣ�������0���ȣ�$\frac{��}{2}$��
��2��ѡ��ii���й�ϵʽ
��S=AM•AN=��3+$\frac{2}{tan��}$��•��2+3tan�ȣ�����0���ȣ�$\frac{��}{2}$����
��S=12+9tan��+$\frac{4}{tan��}$��12+2$\sqrt{9tan��•\frac{4}{tan��}}$=24��
���ҽ���9tan��=$\frac{4}{tan��}$����tan��=$\frac{2}{3}$ʱ��ȡ�Ⱥţ���ʱAN=4
�𣺵�AN�ij���Ϊ4��ʱ������AMPN�������С����СֵΪ24m2��
���� ���⿼���˻�������ʽ����ֵ�е�Ӧ�ã�����ѧ���ļ���������������ε�֪ʶ����һ���е��⣮


 �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | -3 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?x�ʣ�0���У���ʹsinx=tanx | |
| B�� | ���������x��R��x2+x+1��0���ķ��ǡ�����x0��R��x02+x0+1��0�� | |
| C�� | ?�ȡ�R������f��x��=sin��2x+�ȣ�������ż���� | |
| D�� | ��ABC�У���sinA+sinB=cosA+cosB���ǡ�C=$\frac{��}{2}$���ij�Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������������������ | B�� | ����$\overrightarrow{a}$���ߵ����� | ||
| C�� | ����$\overrightarrow{c}$���ߵ����� | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com