���𰸡�
��������1����a=1��b=2���ɵ�f��x��=x+2������f��x�������������ҵ�x��[a
n-1��b
n-1]ʱֵ��Ϊ[a
n��b
n]��
�ɵõ�n��2ʱ��a
n=f��a
n-1��=a
n-1+2��b
n=f��b
n-1��=b
n-1+2����a
1��b
1�����õȲ����е�ͨ�ʽ���ɵó���
��2����a��0ʱ������f��x��=ax+b�����������ɵõ�n��2ʱ��b
n=f��b
n-1��=ab
n-1+b����*��
����b
n=b
n-1ʱ��b
n=1��b=1-a����b��1-a��a��0��a��1��������������{b
n}�Ĺ���Ϊq��b
1=1�����ڣ�*���ֱ�ȡn=2��3�ɵ�
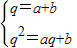
���ɽ��b��ֵ��
��3����a��0ʱ������f��x��=ax+b�����������ɵõ�n��2ʱ��a
n=f��a
n-1��=aa
n-1+b��b
n=f��b
n-1��=ab
n-1+b��
�ٵ�a=1ʱ��a
n=0+��n-1��•b��b
n=1+��n-1��b����b
n-a
n=1���ɵó�T
n-S
n��
�ڵ�a��1ʱ����
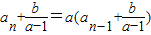
��
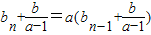
��
�ɵ�
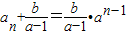
��
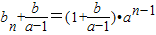
���ɵ�
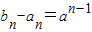
������T
n-S
n=1+a+a
2+��+a
n-1��
����⣺��1����a=1��b=2����f��x��=x+2��
�ߺ���f��x�������������ҵ�x��[a
n-1��b
n-1]ʱֵ��Ϊ[a
n��b
n]��
�൱n��2ʱ��a
n=f��a
n-1��=a
n-1+2��b
n=f��b
n-1��=b
n-1+2��
��a
1=0��b
1=1��
��a
n=0+��n-1��×2=2n-2��b
n=1+��n-1��×2=2n-1��
��a
n=2n-2��b
n=2n-1��
��2����a��0ʱ������f��x��=ax+b�����������൱n��2ʱ��b
n=f��b
n-1��=ab
n-1+b����*��
��b
n=b
n-1ʱ��b
n=1��b=1-a��
���b��1-a��a��0��a��1����
������{b
n}�Ĺ���Ϊq����b
1=1�����ڣ�*���ֱ�ȡn=2��3�ɵ�
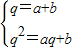
��Ϊb��a+b-1��=0����a+b-1��0����b=0��
�ʵ�b=0ʱ����{b
n}�ǹ��Ȳ�Ϊ1�ĵȱ����У�
���b=0��
��3����a��0ʱ������f��x��=ax+b����������
�൱n��2ʱ��a
n=f��a
n-1��=aa
n-1+b��b
n=f��b
n-1��=ab
n-1+b��
�ٵ�a=1ʱ��a
n=0+��n-1��•b��b
n=1+��n-1��b��
��T
n-S
n=1+1+��+1=n��
�ڵ�a��1ʱ����
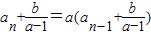
��
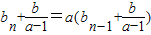
��
�ɵ�
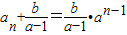
��
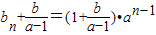
��
��ɵ�
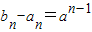
��
��T
n-S
n=1+a+a
2+��+a
n-1=
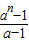
��
���Ͽ�֪����a=1ʱ��T
n-S
n=n��
��a��1ʱ��T
n-S
n=
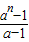
��
��������������һ�κ����ĵ����ԡ��Ȳ�������ȱ����е�ͨ�ʽ����ǰn���ʽ���������۵�˼�뷽���ǽ���Ĺؼ���

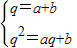 ���ɽ��b��ֵ��
���ɽ��b��ֵ��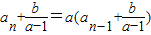 ��
��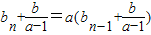 ��
��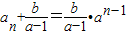 ��
��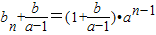 ���ɵ�
���ɵ�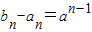 ������Tn-Sn=1+a+a2+��+an-1��
������Tn-Sn=1+a+a2+��+an-1��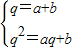
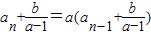 ��
��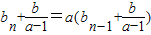 ��
��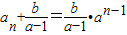 ��
��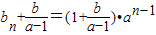 ��
��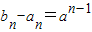 ��
��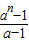 ��
��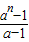 ��
��

