练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列说法错误的是　　

    A. 棱柱的侧面都是平行四边形

    B. 所有面都是三角形的多面体一定是三棱锥

    C. 用一个平面去截正方体，截面图形可能是五边形

    D. 将直角三角形绕其直角边所在直线旋转一周所得的几何体是圆锥

    【答案】B

    【解析】

    由棱柱的性质可判断A；可举正八面体可判断B；用一个平面去截正方体，与正方体的五个面相交，可判断C；由圆锥的定义可判断D．

    由棱柱的性质可得棱柱的侧面都是平行四边形，则A正确；

    所有面都是三角形的多面体不一定是三棱锥，比如正八面体的各个面都是正三角形，则B错误；

    用一个平面去截正方体，与正方体的五个面相交，可得截面图形是五边形，则C正确；

    由圆锥的定义可得直角三角形绕其直角边所在直线旋转一周所得的几何体是圆锥，则D正确．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知两个不共线的向量满足， ， .

    （1）若与垂直，求的值；

    （2）当时，若存在两个不同的使得成立，求正数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列中，在直线．

    （1）求数列{an}的通项公式；

    （2）令，数列的前n项和为．

    （ⅰ）求；

    （ⅱ）是否存在整数λ，使得不等式(－1)nλ＜ (n∈N)恒成立？若存在，求出λ的取值的集合；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数．

    (1)若函数在上单调递增，求的取值范围；

    (2)当时，设函数的最小值为，求证：；

    (3)求证：对任意的正整数，都有．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数满足，且的最小值是.

    （1）求的解析式；

    （2）若关于的方程在区间上有唯一实数根，求实数的取值范围；

    （3）函数，对任意都有恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.

    根据该折线图,下列结论错误的是(　　)

    A. 月接待游客量逐月增加

    B. 年接待游客量逐年增加

    C. 各年的月接待游客量高峰期大致在7,8月

    D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知中心在原点的双曲线的右焦点为,右顶点为.

    （1）求双曲线的方程；

    （2）若直线与双曲线恒有两个不同的交点和，且(其中为坐标原点)，求实数取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥的底面为平行四边形，且,, 分别为中点，过作平面分别与线段相交于点.

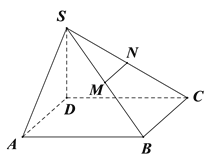
    （Ⅰ）在图中作出平面使面‖ (不要求证明）；

    （II）若，在（Ⅰ）的条件下求多面体的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】燕山公园计划改造一块四边形区域铺设草坪，其中百米，百米，，，草坪内需要规划4条人行道以及两条排水沟，其中分别为边的中点．

    （1）若，求排水沟的长；

    （2）当变化时，求条人行道总长度的最大值．

    查看答案和解析>>

    同步练习册答案