
| A. | [0,$\frac{1}{8}$) | B. | [$\frac{1}{8}$,1) | C. | [1,8) | D. | [8,+∞) |
分析 根据基本不等式得到则$\frac{1}{a}$-1≥$\frac{2\sqrt{bc}}{a}$,$\frac{1}{b}$-1≥$\frac{2\sqrt{ac}}{b}$,$\frac{1}{c}$-1≥$\frac{2\sqrt{ab}}{c}$继而求出M的范围
解答 解:根据题意,a+b+c=1,则$\frac{1}{a}$-1=$\frac{a+b+c}{a}$-1=$\frac{b+c}{a}$≥$\frac{2\sqrt{bc}}{a}$,
同理$\frac{1}{b}$-1≥$\frac{2\sqrt{ac}}{b}$,$\frac{1}{c}$-1≥$\frac{2\sqrt{ab}}{c}$,
则M=($\frac{1}{a}$-1)($\frac{1}{b}$-1)($\frac{1}{c}$-1)≥$\frac{2\sqrt{bc}}{a}$•$\frac{2\sqrt{ac}}{b}$•$\frac{2\sqrt{ab}}{c}$=8,当且仅当a=b=c=$\frac{1}{3}$时取等号.
则($\frac{1}{a}$-1)($\frac{1}{b}$-1)($\frac{1}{c}$-1)有最小值为8,
则M的取值范围是[8,+∞),
故选:D.
点评 本题考查了基本不等式的应用,属于基础题


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-∞,e+2) | C. | (-∞,0)∪(e+2,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4\sqrt{5}}{5}$ | D. | $\frac{16}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
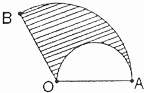 如图,在圆心角为120°的扇形OAB中,以OA为直径作一个半圆,若在扇形OAB内随机取一点,则此点取自阴影部分的概率是( )
如图,在圆心角为120°的扇形OAB中,以OA为直径作一个半圆,若在扇形OAB内随机取一点,则此点取自阴影部分的概率是( )| A. | $\frac{5}{8π}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{8π}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com