
分析 由S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}$bcsin60°=10$\sqrt{3}$,可解得bc=40,由余弦定理知:a2=b2+c2-2bccosA,从而解得b2+c2=89,从而(b+c)2=b2+c2+2bc=169,从而解得b+c=13,即可求得周长.
解答 解:∵S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}$bcsin60°=10$\sqrt{3}$,
∴bc=40,
由余弦定理知:a2=b2+c2-2bccosA,从而有49=b2+c2-bc,解得b2+c2=89,
∴(b+c)2=b2+c2+2bc=89+80=169,从而解得b+c=13.
∴△ABC的周长为:13+7=20.
故答案为:20.
点评 解决三角形问题,正、余弦定理是我们常用的定理,利用余弦定理,通常需知道三角形的两边及其夹角或已知三边,本题属于基本知识的考查.


科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(理)试卷(解析版) 题型:解答题
选修4-1:几何证明选讲
如图,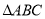 的外接圆为
的外接圆为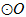 ,延长
,延长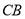 至
至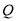 ,再延长
,再延长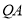 至
至 ,使得
,使得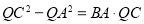 .
.
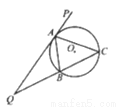
(1)求证: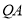 为
为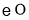 的切线;
的切线;
(2)若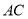 恰好为
恰好为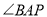 的平分线,
的平分线,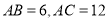 ,求
,求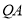 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -12 | B. | -9 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{27}$ | B. | $-\frac{1}{27}$ | C. | ±$\frac{1}{27}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com